【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).

(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 .(直接写出答案)
参考答案:
【答案】(1) y=﹣x2+2x+3;(2) ![]() ;(3)x=±
;(3)x=±![]() 或x=±2;(4)x=±
或x=±2;(4)x=±![]() .
.
【解析】分析:(1)用待定系数法求出抛物线解析式即可;(2)先确定出直线AB解析式,进而得出点D,C的坐标,即可得出CD的函数关系式,即可得出结论;(3)先确定出CD=|-x2+3x|,DP=|-x+3|,再分两种情况解绝对值方程即可;
(4)利用四个点在同一个圆上,得出过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,建立方程即可.
本题解析:
(1)∵抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),∴﹣9+3b+c=0,c=3,∴b=2,∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(3,0),B(0,3),∴直线AB解析式为y=﹣x+3,
∵P(x,0).∴D(x,﹣x+3),C(x,﹣x2+2x+3),
∵0<x<3,∴CD=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,当x=
,当x=![]() 时,CD最大=
时,CD最大=![]() ;
;
(3)由(2)知,CD=|﹣x2+3x|,DP=|﹣x+3|
①当S△PDB=2S△CDB时,∴PD=2CD,即:2|﹣x2+3x|=|﹣x+3|,∴x=±![]() 或x=3(舍),
或x=3(舍),
②当2S△PDB=S△CDB时,∴2PD=CD,即:|﹣x2+3x|=2|﹣x+3|,∴x=±2或x=3(舍),
即:综上所述,x=±![]() 或x=±2;
或x=±2;
(4)直线AB解析式为y=﹣x+3,∴线段AB的垂直平分线l的解析式为y=x,
∵过点B,C,P的外接圆恰好经过点A,
∴过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,
∴![]() ,∴x=±
,∴x=±![]() ,故答案为:
,故答案为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的相反数大于它本身,这个数是( )
A.正数B.负数C.0D.非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市旧房改造对632000m2外墙保暖,将632000用科学记数法表示为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.同位角相等B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角D.在同一平面内,如果a∥b,b∥c,则a∥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】“淄博地区明天降水概率是15%”,下列说法中,正确的是( )
A.淄博地区明天降水的可能性较小
B.淄博地区明天将有15%的时间降水
C.淄博地区明天将有15%的地区降水
D.淄博地区明天肯定不降水 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长分别为2、x、3,则x可能是( )
A.5B.1C.6D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.
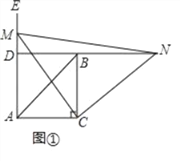

(1)问题发现:直接写出∠NDE= 度;
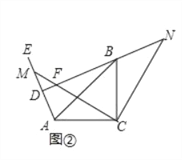
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.
(3)如图③,若∠EAC=15°,BD=
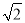 ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
相关试题

