Question

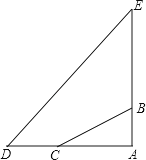
【题目】已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．
（1）求证：△ACE≌△BCD；
（2）求证：2CD2=AD2+DB2 ．

Answer 1

【答案】
（1）

证明：∵△ABC和△ECD都是等腰直角三角形，

∴AC=BC，CD=CE，

∵∠ACB=∠DCE=90°，

∴∠ACE+∠ACD=∠BCD+∠ACD，

∴∠ACE=∠BCD，

在△ACE和△BCD中，

，

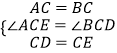∴△AEC≌△BDC（SAS）

（2）

证明：∵△ACB是等腰直角三角形，

∴∠B=∠BAC=45度．

∵△ACE≌△BCD，

∴∠B=∠CAE=45°

∴∠DAE=∠CAE+∠BAC=45°+45°=90°，

∴AD2+AE2=DE2．

由（1）知AE=DB，

∴AD2+DB2=DE2，即2CD2=AD2+DB2

【解析】（1）本题要判定△ACE≌△BCD，已知△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，则DC=EA，AC=BC，∠ACB=∠ECD，又因为两角有一个公共的角∠ACD，所以∠BCD=∠ACE，根据SAS得出△ACE≌△BCD；
　　　　（2）由（1）的论证结果得出∠DAE=90°，AE=DB，从而求出AD2+DB2=DE2 ， 即2CD2=AD2+DB2 ． 本题考查了全等三角形的判定与性质，等腰直角三角形的性质，以及等角的余角相等的性质，熟记各性质是解题的关键．