搜索
【题目】如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E．若BC=6，则DE的长为（ ）
A. 1 B. 2 C. 3 D. 4
参考答案：
【答案】B
【解析】首先根据角平分线的性质得到DE=DC，∠BAD=∠CAD，由垂直平分线的性质可得AD=BD，结合等边对等角和等量代换的知识可得∠B=∠BAD=∠CAD；然后根据∠C=90°，即可求得∠B=30°，在Rt△BDE中，然后根据含有30°角的直角三角形的性质，得出BD=2DE，即可解答.
解：∵AD平分∠BAC，∠C=90°，DE⊥AB，
∴DE=DC，∠B+∠BAC=90°，∠BAD=∠CAD，
∵DE是AB的中垂线，
∴AD=BD，
∴∠B=∠BAD，
∴∠B=∠BAD=∠CAD=30°.
∵在Rt△BDE中∠B=30°，
∴BD=2DE=2DC，
∵BC=6，
∴DE=DC=2.
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：如果⊙C的半径为r，⊙C外一点P到⊙C的切线长小于或等于2r，那么点P叫做⊙C的“离心点”.
（1）当⊙O的半径为1时，
①在点P1（
， 
），P2（0，－2），P3（
，0）中，⊙O的“离心点”是 ；②点P（m，n）在直线
上，且点P是⊙O的“离心点”，求点P横坐标m的取值范围；（2）⊙C的圆心C在y轴上，半径为2，直线
与x轴、y轴分别交于点A，B. 如果线段AB上的所有点都是⊙C的“离心点”，请直接写出圆心C纵坐标的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有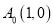点
，点
第一次跳动至点
，第二次点
跳动至点
，第三次点
跳动至点
，第四次点
跳动至点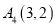
，……依此规律跳动下去，则点
与点
之间的距离是（ ）
A. 2021B. 2020C. 2019D. 2018
-
科目： 来源： 题型：
查看答案和解析>>【题目】小岩打算购买气球装扮学校“毕业典礼”活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同.由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为______元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在等边三角形ABC中，BC=6cm，射线AG//BC，点E从点A出发，沿射线AG以1cm/s的速度运动，同时点F从点B出发，沿射线BC以2cm/s的速度运动，设运动时间为t，当t为( )s时，以A，F，C，E为顶点的四边形是平行四边形？（ ）
A.2B.3C.6D.2或6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P从
出发，沿所示方向运动，每当碰到长方形OABC的边时会进行反弹，反弹时反射角等于入射角，当点P第2018次碰到长方形的边时，点P的坐标为______．
【答案】
【解析】
根据反射角与入射角的定义作出图形；由图可知，每6次反弹为一个循环组依次循环，用2018除以6，根据商和余数的情况确定所对应的点的坐标即可．
解：如图所示：经过6次反弹后动点回到出发点
，
，
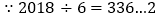当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹，点P的坐标为
．故答案为：
．【点睛】
此题主要考查了点的坐标的规律，作出图形，观察出每6次反弹为一个循环组依次循环是解题的关键．
【题型】填空题
【结束】
15【题目】为了保护环境，某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆，其中A种型号每辆价格为a万元，每年节省油量为
万升；B种型号每辆价格为b万元，每年节省油量为
万升：经调查，购买一辆A型车比购买一辆B型车多20万元，购买2辆A型车比购买3辆B型车少60万元．
请求出a和b；
若购买这批混合动力公交车每年能节省
万升汽油，求购买这批混合动力公交车需要多少万元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-1，3），B（-2，1），C（-3，1）．
（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1C1A1的值；
（2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出将△ABC放大后的△A2B2C2，并写出A2点的坐标；
（3）若点D为线段BC的中点，直接写出经过（2）的变化后点D的对应点D2的坐标．
相关试题
