Question

【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．

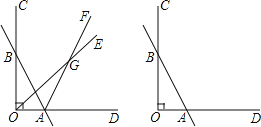
（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=30°，则∠OGA=

（2）若∠GOA=∠BOA，∠GAD=∠BAD，∠OBA=30°，则∠OGA=

（3）将（2）中“∠OBA=30°”改为“∠OBA=α”，其余条件不变，则∠OGA= α （用含α的代数式表示）

（4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO=α（30°＜α＜90°），求∠OGA的度数（用含α的代数式表示）

Answer 1

【答案】（1）15°；

（2）10°；

（3）；

（4）∠OGA的度数为α+15°或α﹣15°

【解析】

试题分析：（1）由于∠BAD=∠ABO+∠BOA=α+90°，由AF平分∠BAD得到∠FAD=∠BAD，而∠FAD=∠EOD+∠OGA，2×45°+2∠OGA=α+90°，则∠OGA=α，然后把α=30°代入计算即可；

（2）由于∠GOA=∠BOA=30°，∠GAD=∠BAD，∠OBA=α，根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°，则∠OGA=α，然后把α=30°代入计算；

（3）由（2）得到∠OGA=α；

（4）讨论：当∠EOD：∠COE=1：2时，利用∠BAD=∠ABO+∠BOA=α+90°，∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=α+90°，则∠OGA=α+15°；

当∠EOD：∠COE=2：1时，则∠EOD=60°，同理得∠OGA=α﹣15°．

解：（1）15°；

（2）10°；

（3）；

（4）当∠EOD：∠COE=1：2时，

则∠EOD=30°，

∵∠BAD=∠ABO+∠BOA=α+90°，

而AF平分∠BAD，

∴∠FAD=∠BAD，

∵∠FAD=∠EOD+∠OGA，

∴2×30°+2∠OGA=α+90°，

∴∠OGA=α+15°；

当∠EOD：∠COE=2：1时，则∠EOD=60°，

同理得到∠OGA=α﹣15°，

即∠OGA的度数为α+15°或α﹣15°．

故答案为15°，10°，α．