【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
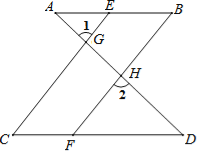
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
参考答案:
【答案】对顶角相等
同位角相等,两直线平行
∠C
两直线平行,同位角相等
内错角相等,两直线平行
【解析】试题分析:由对顶角相等可得∠1=∠CGD,则∠2=∠CGD,根据平行线的判定得到CE∥BF,则∠C=∠BFD,易得∠B=∠BFD,然后根据平行线的判定即可得到AB∥CD.
试题解析:
∵∠1=∠2(已知),且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD (等量代换),
∴CE∥BF (同位角相等,两直线平行),
∴∠BFD=∠C(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠BFD=∠B(等量代换),
∴AB∥CD (内错角相等,两直线平行)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,1)、B(﹣1,b)都在函数
 (x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.

(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:
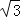 (指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,
(指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,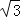 ≈1.732).
≈1.732).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
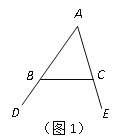
【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;
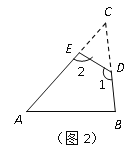
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .
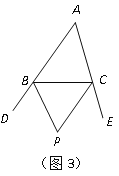
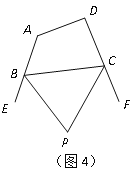
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】廉贻中学为每个学生编号,设定末尾用1表示男生,用2表示女生。如果152132表示“2015年入学的2班13号的同学,是位女生”,那么今年入学的3班19号男生的编号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x+3)=﹣2
相关试题

