【题目】如果(a﹣1)x|a|+1+6=0是关于x的一元二次方程,那么a=_____
参考答案:
【答案】-1
【解析】
直接利用绝对值的性质以及一元二次方程的定义分析得出答案.
∵(a﹣1)x|a|+1+6=0是关于x的一元二次方程,
∴|a|+1=2,a﹣1≠0,
解得:a=﹣1.
故答案为:﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
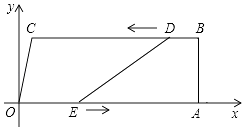
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,四边形OEDC是平行四边形?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在函数y=﹣x2﹣1的图象上的是( )
A.(﹣1,0)B.(1,0)C.(0,﹣1)D.(2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“用两颗钉子在一面墙上钉木条,木条不动”,若用数学知识解释,则其理由是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是全国最大的瓷碗造型建筑坐落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物的横断面(瓷碗横断面ABCD为等腰梯形)的高度如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44的小坡PQ步行到点Q(此过程中AD、AP、PQ始终处于同一平面)后测得点D的仰角减少了5°.
已知坡PQ的水平距离为20米,小敏身高忽略不计.
(1)试计算该瓷碗建筑物的高度?
(2)小敏测得AD与水平面夹角约为58°,底座直径AB约为20米,试计算碗口CD的直径为多少米?
坡度:坡与水平线夹角的正切值.
参考数据:sin40°≈0.64,tan40°≈0.84,sin58°≈0.85,tan58°≈1.60.



-
科目: 来源: 题型:
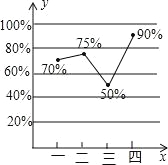
查看答案和解析>>【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣1时,代数式x2+2x+1的值是( )
A.﹣2
B.﹣1
C.0
D.4
相关试题

