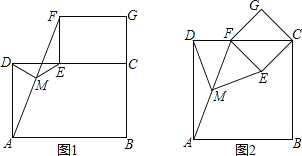
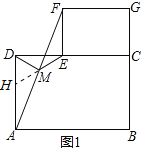
【题目】猜想与证明:如图1摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
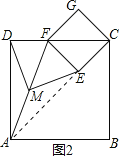
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
参考答案:
【答案】DM=ME,证明过程见解析;(1)、DM=ME;(2)、DM=ME,证明过程见解析.
【解析】
试题分析:延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.
试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,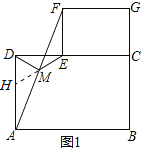
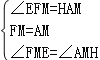
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=DE,
∴DM=HM=ME,
∴DM=ME.
(1)、如图1,延长EM交AD于点H,
∵四边形ABCD和CEFG是矩形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,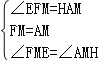
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM
∴DM=HM=ME,
∴DM=ME,
(2)、如图2,连接AE,
∵四边形ABCD和ECGF是正方形,
∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,
在RT△ADF中,AM=MF,
∴DM=AM=MF,
在RT△AEF中,AM=MF,
∴AM=MF=ME,
∴DM=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式3(a2-2ab-b2)-(a2+mab+2b2)中不含有ab项,则m=___
-
科目: 来源: 题型:
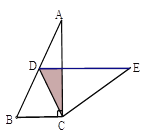
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时点D在AB边上,斜边DE交AC于点F,则n=_______; 图中阴影部分的面积为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】可以把抛物线y=x2平移后得到y=(x+2)2﹣3,则下列平移过程正确的是( )
A. 向左移2个单位,下移3个单位
B. 向右移2个单位,上移3个单位
C. 向右移2个单位,下移3个单位
D. 向左移2个单位,上移3个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】底面直径和高都是1的圆柱侧面积为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的两边长分别为AB=9、AC=2,第三边BC的长为奇数,则( )
A.BC=5
B.BC=7
C.BC=9
D.BC=11 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图形都是轴对称图形,其中对称轴最多的是( )
A.等腰直角三角形
B.直线
C.等边三角形
D.正方形
相关试题

