【题目】(2016浙江省舟山市第24题)小明的爸爸和妈妈分别驾车从家同时出发去上班,爸爸行驶到甲处时,看到前面路口时红灯,他立即刹车减速并在乙处停车等待,爸爸驾车从家到乙处的过程中,速度v(m/s)与时间t(s)的关系如图1中的实线所示,行驶路程s(m)与时间t(s)的关系如图2所示,在加速过程中,s与t满足表达式s=at2
(1)根据图中的信息,写出小明家到乙处的路程,并求a的值;
(2)求图2中A点的纵坐标h,并说明它的实际意义;
(3)爸爸在乙处等代理7秒后绿灯亮起继续前行,为了节约能源,减少刹车,妈妈驾车从家出发的行驶过程中,速度v(m/s)与时间t(s)的关系如图1中的折线O﹣B﹣C所示,行驶路程s(m)与时间t(s)的关系也满足s=at2,当她行驶到甲处时,前方的绿灯刚好亮起,求此时妈妈驾车的行驶速度.

参考答案:
【答案】(1)、180m;a=![]() ;(2)、h=156;表示小明家到甲处的路程为156m;(3)、6m/s
;(2)、h=156;表示小明家到甲处的路程为156m;(3)、6m/s
【解析】
试题分析:(1)、直接利用待定系数法求出抛物线解析式进而得出答案;(2)、利用图形,得出速度和时间,再结合h=48+12×(17﹣8)得出答案;(3)、首先求出OB的解析式进而利用二次函数解析式得出关于x的等式求出答案.
试题解析:(1)、由图象得:小明家到乙处的路程为180m, ∵点(8,48)在抛物线s=at2上,
∴48=a×82, 解得:a=![]() ;
;
(2)、由图及已知得:h=48+12×(17﹣8)=156,
故A点的纵坐标为:156,表示小明家到甲处的路程为156m;
(3)、设OB所在直线的表达式为:v=kt, ∵(8,12)在直线v=kt上, 则12=8k, 解得:k=![]() ,
,
∴OB所在直线的表达式为:v=![]() t,
t,
设妈妈加速所用时间为:x秒, 由题意可得:![]() x2+
x2+![]() x(21+7﹣x)=156,
x(21+7﹣x)=156,
整理得:x2﹣156+208=0, 解得:x1=4,x2=52(不符合题意,舍去), ∴x=4,
∴v=![]() ×4=6(m/s),
×4=6(m/s),
答:此时妈妈驾车的行驶速度为6m/s.
-
科目: 来源: 题型:
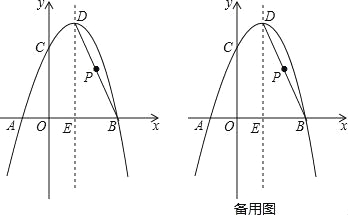
查看答案和解析>>【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5
B.6
C.0.5
D.-6 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9a2(x﹣y)+(y﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20 -
科目: 来源: 题型:
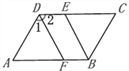
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a-3与a+1互为相反数,那么a= .
相关试题

