【题目】如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数. 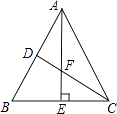
参考答案:
【答案】解:∵AE⊥BC,∴∠AEB=90°. ∵∠B=60°,
∴∠BAE=90°﹣60°=30°.
∴∠CAE=50°﹣30°=20°
∵∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°﹣∠BAC﹣∠B=70°.
又∵CD平分∠ACB,
∴∠ACD= ![]() ∠ACB=35°.
∠ACB=35°.
∴∠AFC=180°﹣35°﹣20°=125°.
【解析】先根据垂直的定义求∠BAE的度数,再结合图形根据角的和差求出∠CAE的度数,利用三角形的内角和求∠ACB,因CD平分∠ACB,所以可得∠ACD,最后利用△AFC的内角和为180°,求得∠AFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A.(7m+4n)元
B.28mn元
C.(4m+7n)元
D.11mn元 -
科目: 来源: 题型:
查看答案和解析>>【题目】H7N9病毒的长度约为0.000065mm,用科学记数法表示数0.000065为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是__

-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上的A点与表示﹣3的点距离4个单位长度,则A点表示的数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式5x4y和25xnym是同类项,则m+n的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2+2(k﹣3)x+9是完全平方式,则k= .
相关试题

