【题目】在长方形![]() 中,
中,![]() ,现将长方形
,现将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置(
的位置(![]() 的对应点为
的对应点为![]() ,其它类似).
,其它类似).
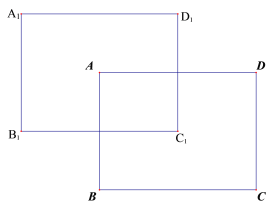
![]() 当
当![]() 时,请画出平移后的长方形
时,请画出平移后的长方形![]() ,并求出长方形
,并求出长方形![]() 与长方形
与长方形![]() 的重叠部分的面积.
的重叠部分的面积.
![]() 当
当![]() 满足什么条件时,长方形
满足什么条件时,长方形![]() 与长方形
与长方形![]() 有重叠部分(边与边叠合不算在内),请用
有重叠部分(边与边叠合不算在内),请用![]() 的代数式表示重叠部分的面积.
的代数式表示重叠部分的面积.
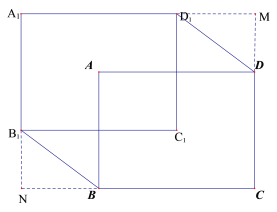
![]() 在平移的过程中,总会形成一个六边形
在平移的过程中,总会形成一个六边形![]() ,试用
,试用![]() 来表示六边形
来表示六边形![]() 的面积.
的面积.
参考答案:
【答案】(1)长方形![]() 见详解,重叠部分的面积=
见详解,重叠部分的面积=![]() ;(2)重叠部分的面积=
;(2)重叠部分的面积=![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,画出长方形![]() ,进而可得重叠部分的面积;
,进而可得重叠部分的面积;
(2)根据题意得长方形![]() 与长方形
与长方形![]() 的重叠部分的长为
的重叠部分的长为![]() ,宽为
,宽为![]() ,从而得重叠部分的面积,由重叠部分的长与宽的实际意义,列出关于x的不等式组,进而即可求解;
,从而得重叠部分的面积,由重叠部分的长与宽的实际意义,列出关于x的不等式组,进而即可求解;
(3)延长A1D1,CD交于点M,延长A1B1,CB交于点N,根据割补法,求出六边形![]() 的面积,即可.
的面积,即可.
(1)长方形![]() ,如图所示:
,如图所示:
∵在长方形![]() 中,
中,![]() ,将长方形
,将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置,
的位置,
∴长方形![]() 与长方形
与长方形![]() 的重叠部分的面积=
的重叠部分的面积=![]() ;
;
(2)∵![]() ,将长方形
,将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置,
的位置,
∴长方形![]() 与长方形
与长方形![]() 的重叠部分的长为
的重叠部分的长为![]() ,宽为
,宽为![]() ,
,
∴重叠部分的面积=![]() ,
,
∵![]() 且
且![]() 且
且![]() ,
,
∴![]() ;
;
(3)延长A1D1,CD交于点M,延长A1B1,CB交于点N,
六边形![]() 的面积=
的面积=![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx(k<0)与双曲线
 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
【答案】-6
【解析】试题分析:∵点A(x1,y1),B(x2,y2)是双曲线y=
 上的点,
上的点,∴x1y1=x2y2=-3①,
∵直线y=kx(k<0)与双曲线y=
 交于点A(x1,y1),B(x2,y2)两点,
交于点A(x1,y1),B(x2,y2)两点,∴x1=-x2,y1=-y2②,
∴原式=-3x1y1+5x2y2=9-15=-6.
故答案为:-6.
点睛:本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.
【题型】填空题
【结束】
15【题目】A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了 50%,而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h,则根据题意可列方程为 _____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识,回答下列问题:(图中的数字表示每一级台阶的高度(单位:
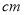 )).
)).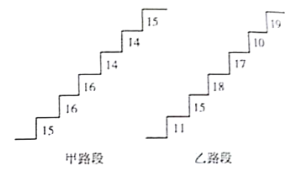
(1)请分别求出甲、乙两段路段每一级台阶高度的平均数.
(2)哪段台阶路走起来更舒服?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
 的解是
的解是 ,
, ;
; 即
即 的解是
的解是 ;
; 的解是
的解是 ,
, ;
; 的解是
的解是 ,
, ;
;
 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=
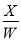 ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
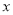 分别等于3和
分别等于3和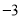 时,多项式
时,多项式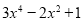 的值是( )
的值是( )A.相等B.互为倒数C.互为相反数D.异号
相关试题

