【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+5与x轴交于A（1，0）、B（5，0）两点，点D是抛物线上横坐标为6的点．点P在这条抛物线上，且不与A、D两点重合，过点P作y轴的平行线与射线AD交于点Q，过点Q作QF垂直于y轴，点F在点Q的右侧，且QF=2，以QF、QP为邻边作矩形QPEF．设矩形QPEF的周长为d，点P的横坐标为m．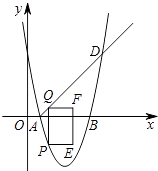

（1）求这条抛物线所对应的函数表达式．
（2）求这条抛物线的对称轴将矩形QPEF的面积分为1：2两部分时m的值．
（3）求d与m之间的函数关系式及d随m的增大而减小时d的取值范围．
（4）当矩形QPEF的对角线互相垂直时，直接写出其对称中心的横坐标．

参考答案：

【答案】
（1）

解：把A（1，0）、B（5，0）代入y=ax2+bx+5，

，

解得 ，

∴y=x2﹣6x+5


（2）

解：如图所示：∵抛物线y=x2﹣6x+5的对称轴为：x=﹣ =﹣ =3，

∵这条抛物线的对称轴将矩形QPEF的面积分为1：2两部分，

可得PN=3﹣m，PE=2，

∴ = 或 = ，

解得：m= 或m=


（3）

解：当x=6时，y=x2﹣6x+5=62﹣6×6+5=5，

∴点D的坐标为（6，5）．

射线AD所对应的函数表达式为y=x﹣1（x＞1）．

∴P（m，m2﹣6m+5），Q（m，m﹣1）．

当1＜m＜6时，d=2（﹣m2+7m﹣6+2）=﹣2m2+14m﹣8，

当m＞6时，d=2（m2﹣7m+6+2）=2m2﹣14m+16，

又d=﹣2m2+14m﹣8=﹣2（m﹣ ）2+ ，

∴d随m的增大而减小时d的取值范围是4＜d≤


（4）

解：当矩形QPEF的对角线互相垂直时，则矩形QPEF是正方形，边长为2，

当1＜m＜6时，m﹣1﹣（m2﹣6m+5）=2，

整理得：m2﹣7m+8=0，

解得：m1= ，m2= ，

当m＞6时，m2﹣6m+5﹣（m﹣1）=2，

整理得：m2﹣7m+4=0，

解得：m3= ，m4= （舍去），

故其对称中心的横坐标为： +1= ， +1= ， +1=


【解析】（1）直接利用待定系数法求出二次函数解析式即可；（2）首先求出函数对称轴进而得出m的值；（3）分别利用当1＜m＜6时，d=2（﹣m2+7m﹣6+2），当m＞6时，d=2（m2﹣7m+6+2）求出d的取值范围即可；（4）当矩形QPEF的对角线互相垂直时，则矩形QPEF是正方形，边长为2，进而得出m的值求出答案．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

关闭