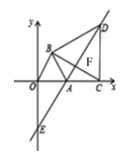
【题目】在直角坐标系中，O为坐标原点，点A坐标为（2，0），以OA为边在第一象限内作等边△OAB，C为x轴正半轴上的一个动点（OC＞2），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．

（1）求证：△OBC≌△ABD

（2）随着C点的变化，直线AE的位置变化吗？若变化，请说明理由；若不变，请求出直线AE的解析式．

（3）以线段BC为直径作圆，圆心为点F，当C点运动到何处时，直线EF∥直线BO；这时⊙F和直线BO的位置关系如何？请给予说明．

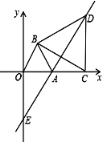
【答案】（1）见解析；（2）直线AE的位置不变，AE的解析式为：；（3）C点运动到处时，直线EF∥直线BO；此时直线BO与⊙F相切，理由见解析.

【解析】

（1）由等边三角形的性质可得到OB=AB，BC=BD，∠OBA=∠DBC，等号两边都加上∠ABC，得到∠OBC=∠ABD，根据“SAS”得到△OBC≌△ABD.（2）先由三角形全等，得到∠BAD=∠BOC=60°，由等边△BCD，得到∠BAO=60°，根据平角定义及对顶角相等得到∠OAE=60°，在直角三角形OAE中，由OA的长，根据tan60°的定义求出OE的长，确定出点E的坐标，设出直线AE的方程，把点A和E的坐标代入即可确定出解析式.（3）由EA∥OB，EF∥OB，根据过直线外一点作已知直线的平行线有且只有一条，得到EF与EA重合，所以F为BC与AE的交点，又F为BC的中点，得到A为OC中点，由A的坐标即可求出C的坐标；相切理由是由F为等边三角形BC边的中点，根据“三线合一”得到DF与BC垂直，由EF与OB平行得到BF与OB垂直，得证.

（1）证明：∵△OAB和△BCD都为等边三角形，
∴OB=AB，BC=BD，∠OBA=∠DBC=60°，

∴∠OBA+∠ABC=∠DBC+∠ABC，
即∠OBC=∠ABD，

在△OBC和△ABD中，

,

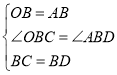∴△OBC≌△ABD.

（2）随着C点的变化，直线AE的位置不变，

∵△OBC≌△ABD，

∴∠BAD=∠BOC=60°，
又∵∠BAO=60°，

∴∠DAC=60°，
∴∠OAE=60°，又OA=2，
在Rt△AOE中，tan60°=，
则OE=2，

∴点E坐标为（0，-2），

设直线AE解析式为y=kx+b，把E和A的坐标代入得：

，

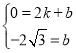解得， ，

∴直线AE的解析式为：.

（3）C点运动到处时，直线EF∥直线BO；此时直线BO与⊙F相切，理由如下：
∵∠BOA=∠DAC=60°，EA∥OB，又EF∥OB，
则EF与EA所在的直线重合，

∴点F为DE与BC的交点，
又F为BC中点，

∴A为OC中点，又AO=2，则OC=4，
∴当C的坐标为（4，0）时，EF∥OB，
这时直线BO与⊙F相切，理由如下：
∵△BCD为等边三角形，F为BC中点，
∴DF⊥BC，又EF∥OB，
∴FB⊥OB，

∴直线BO与⊙F相切，

关闭