【题目】正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E逆时针旋转90度,得到EF,连接AF,FC,则FC=____.

参考答案:
【答案】![]()
【解析】
作FH⊥CD于H,如图,利用正方形的性质得DA=CD,∠D=90°,再根据旋转的性质得EA=EF,∠AEF=90°,接着证明△ADE≌△EHF得到DE=FH=1,AD=EH,所以EH=DC,则DE=CH=1,然后利用勾股定理计算FC的长.
解:作FH⊥CD于H,如图,
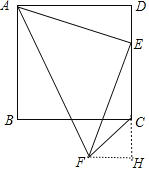
∵四边形ABCD为正方形,
∴DA=CD,∠D=90°,
∵AE绕点E逆时针旋转90°得到EF,
∴EA=EF,∠AEF=90°,
∵∠DAE+∠AED=90°,∠FEH+∠AED=90°,
∴∠EAD=∠FEH,
在△ADE和△EHF中
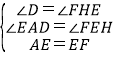
∴△ADE≌△EHF,
∴DE=FH=1,AD=EH,
∴EH=DC,
即DE+CE=CH+EC,
∴DE=CH=1,
在Rt△CFH中,FC![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
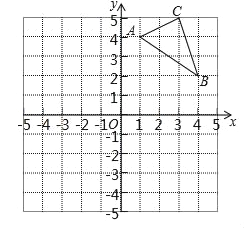
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个小方格的边长均为1个单位长度).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并求出点B旋转到点B2所经过的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式.
①4×1×2+1=(1+2)2;②4×2×3+1=(2+3)2;③4×3×4+1=(3+4)2…
(1)根据你观察、归纳,发现的规律,写出4×2016×2017+1可以是哪个数的平方?
(2)试猜想第n个等式,并通过计算验证它是否成立.
(3)利用前面的规律,将4(
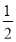 x2+x)(
x2+x)(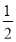 x2+x+1)+1因式分解.
x2+x+1)+1因式分解. -
科目: 来源: 题型:
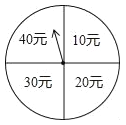
查看答案和解析>>【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学公益组织计划购买
 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买 套装比购买
套装比购买 套装多用20元,且购买5套
套装多用20元,且购买5套 套装和4套
套装和4套 套装共需820元.
套装共需820元.(1)求购买一套
 套装文具、一套
套装文具、一套 套装各需要多少元?
套装各需要多少元?(2)根据该公益组织的募捐情况和捐助对象情况,需购买
 两种套装共60套,要求购买
两种套装共60套,要求购买 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买 套装最多多少套?
套装最多多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

相关试题

