【题目】如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③∠DFC=∠ADC﹣∠DCE;④S△EDF=S△BCF,其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
参考答案:
【答案】D
【解析】试题解析:∵AD∥BC,
∴∠A+∠ABC=180°,∠ADC+∠BCD=180°,
∵∠A=∠BCD,
∴∠ABC=∠ADC,
∵∠A=∠BCD,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∵∠A=∠ABD,DE平分∠ADB,
∴DE⊥AB,
∴DE⊥CD,
∵∠A=∠ABD,四边形ABCD是平行四边形,
∴AD=BD=BC,
∴∠BDC=∠BCD,
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠ADC=∠ADB+∠BDC,
∴∠ADC=∠DBC+∠BCD,
∴∠ADC-∠DCE=∠DBC+∠BCD-∠DCE=∠DBC+∠BCF,
∵∠DFC=∠DBC+BCF,
∴∠DFC=∠ADC-∠DCE;
∵AB∥CD,
∴△BED的边BE上的高和△EBC的边BE上的高相等,
∴由三角形面积公式得:S△BED=S△EBC,
都减去△EFB的面积得:S△EDF=S△BCF,
∴①②③④都正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(-4,y1)、(2,y2)都在直线y=-3x+5上,则y1________y2.(填“>”、“=”或“<”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:24÷(﹣2)3﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,互为相反数的是( )
A. |+2|与|﹣2| B. ﹣|+2|与+(﹣2) C. ﹣(﹣2)与+(+2) D. |﹣(﹣3)|与﹣|﹣3|
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
(1)a= ;
(2)补全条形统计图;
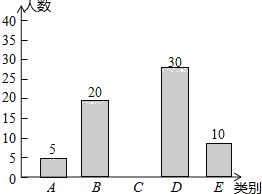
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:y=(k-1)x|k|+k2-4是一次函数,求(3k+2)2 007的值.
相关试题

