Question

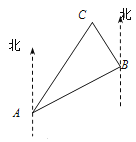
【题目】如图，在一次夏令营活动中，小玲从营地A出发，沿北偏东60°方向走了m到达B点，然后再沿北偏西30°方向走了500m到达目的地C点．（1）求A，C两点之间的距离．（2）确定目的地C在营地A什么方向．

Answer 1

【答案】北偏东30°的方向

【解析】

试题分析：（1）根据直角三角形的勾股定理性质可求解；

（2）根据30°角的直角三角形的性质可求解.

试题解析：（1）如图，

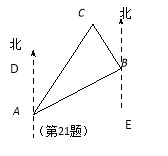
∴∠DAB=∠ABE=60°．

∵30°+∠CBA+∠ABE=180°，∴∠CBA=90°．

在Rt△ABC中，∵BC=500m，AB=m，

由勾股定理可得：AC2=BC2+AB2，

所以AC=1000（m）；

（2）在Rt△ABC中，∵BC=500m，AC=1000m，

∴∠CAB=30°，

∵∠DAB=60°，

∴∠DAC=30°．

即点C在点A的北偏东30°的方向