Question

【题目】如图，已知∠AOB， OE平分∠AOC， OF平分∠BOC.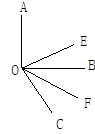

（1）若∠AOB是直角，∠BOC＝60°，求∠EOF的度数；
（2）猜想∠EOF与∠AOB的数量关系；
（3）若∠AOB＋∠EOF＝156°，则∠EOF是多少度？

Answer 1

【答案】
（1）解：∵∠AOC＝∠AOB＋∠BOC，
∴∠AOC＝90°＋60°＝150°.
∵OE平分∠AOC，
∴∠EOC＝150°÷2＝75°.
∵OF平分∠BOC，
∴∠COF＝60°÷2＝30°.
∵∠EOC＝∠EOF＋∠COF,
∴∠EOF＝75°－30°＝45°
（2）解：∵OE平分∠AOC，OF平分∠BOC．
∴∠COE＝ ∠AOC，∠COF＝ ∠BOC
∵∠AOB＝∠AOC－∠BOC
∴∠EOF＝∠COE－∠COF＝ ∠AOC－ ∠BOC＝ （∠AOC－∠BOC）＝ ∠AOB
（3）解：∵OE平分∠AOC，OF平分∠BOC，
∴∠COE＝ ∠AOC，∠COF＝ ∠BOC，
∴∠EOF＝ ∠AOC－ ∠BOC＝ （∠AOC－∠BOC）＝ ∠AOB．又∵∠AOB＋∠EOF＝156°，
∴∠EOF＝52°
【解析】（1）首先求出∠AOC的度数，再根据角平分线的性质计算出∠EOC，∠BOF的度数，然后根据角的和差关系即可算出∠EOF的度数；
（2）根据角平分线的定义得出∠COE＝ ∠AOC，∠COF＝ ∠BOC ，又因∠AOB＝∠AOC－∠BOC ，从而得出∠EOF＝∠COE－∠COF＝ ∠AOC－ ∠BOC＝ （∠AOC－∠BOC）＝ ∠AOB ；
（3）根据角平分线的定义得出∠COE＝ ∠AOC，∠COF＝ ∠BOC ，根据角的和差得出∠EOF＝ ∠AOC－ ∠BOC＝ （∠AOC－∠BOC）＝ ∠AOB．又∠AOB＋∠EOF＝156°，从而得出∠EOF＝52° 。