【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC. 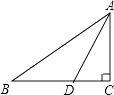
(1)当∠B=40°时,求∠ADC的度数;
(2)若AB=10cm,CD=4cm,求△ABD的面积.
参考答案:
【答案】
(1)解:∵∠C=90°,∠B=40°,
∴∠BAC=50°,
∵AD平分∠BAC,
∴ ![]() ,
,
∴∠ADC=∠B+∠BAD=65°
(2)解:过D作DE⊥AB于E,
∵AD平分∠BAC,
∴DE=CD=4,
∴ ![]() ABDE=
ABDE= ![]() ×10×4=20cm2.
×10×4=20cm2.
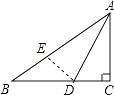
【解析】(1)根据三角形的内角和得到∠BAC=50°,根据三角形的外角的性质即可得到结论;(2)过D作DE⊥AB于E,根据角平分线的性质得到DE=CD=4,由三角形的面积公式即可得到结论.
【考点精析】通过灵活运用三角形的面积和三角形的内角和外角,掌握三角形的面积=1/2×底×高;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(﹣10)+(﹣2)﹣(﹣5)
(2 )﹣7+13﹣6+20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:﹣2(x2﹣3y)﹣[x2﹣3(2x2﹣3y)],其中x和y满足(x+1)2+|y+2|=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
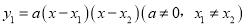 与x轴分别交于A(
与x轴分别交于A(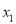 ,0)、B(
,0)、B(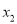 ,0)两点,直线
,0)两点,直线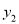 =2x+t经过点A.
=2x+t经过点A.(1)已知A、B两点的横坐标分别为3、
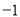 .
.①当a =1时,直接写出抛物线
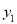 和直线
和直线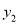 相应的函数表达式;
相应的函数表达式;②如图,已知抛物线
 在3<x<4这一段位于直线
在3<x<4这一段位于直线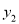 的下方,在5<x<6这一段位于直线
的下方,在5<x<6这一段位于直线 的上方,求a的取值范围;
的上方,求a的取值范围;(2)若函数
 的图像与
的图像与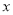 轴仅有一个公共点,探求
轴仅有一个公共点,探求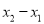 与
与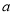 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a﹣3b=﹣3,那么代数式5﹣a+3b的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是
A. 两条直线被第三条直线所截,同位角相等
B. 相等的角是对顶角
C. 过一点有且只有一条直线与已知直线平行
D. 三角形的外角等于与它不相邻的两个内角的和
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学家在实验中检测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( )
A.3.5×10﹣6
B.3.5×106
C.3.5×10﹣5
D.35×10﹣5
相关试题

