搜索
【题目】一组数据：10，15，10，17，18，20．对于这组数据，下列说法错误的是（ ）
A.平均数是15
B.众数是10
C.中位数是17
D.方差是 
参考答案：
【答案】C
【解析】解：A、这组数据的平均数是： 
=15，正确； B、∵10出现了2次，出现的次数最多，∴众数是10，正确；
C、把这些数从小到大排列为10，10，15，17，18，20，则中位数是 
=16，故本选项错误；
D、这组数据的方差是： 
[2×（10﹣15）2+（15﹣15）2+（17﹣15）2+（18﹣15）2+（20﹣15）2]= 
，正确；
故选C．
【考点精析】认真审题，首先需要了解算术平均数(总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数)，还要掌握中位数、众数(中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=ax2﹣2ax﹣3a（a＞0）与x轴交于A、B两点（点A在点B左侧），经过点A的直线l：y=kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
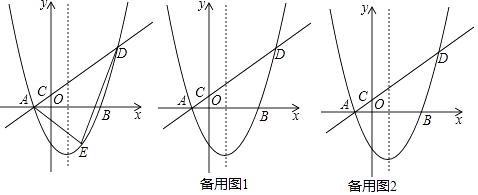
（1）直接写出点A的坐标，并用含a的式子表示直线l的函数表达式（其中k、b用含a的式子表示）．
（2）点E为直线l下方抛物线上一点，当△ADE的面积的最大值为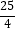
时，求抛物线的函数表达式；
（3）设点P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否为矩形？若能，求出点P的坐标；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为(1，0)，(2，0)，(2，1)，(1，1)，(1，2)，(2，2)，…，根据这个规律，第2 018个点的坐标为( )
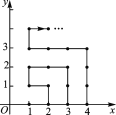
A. (45，9) B. (45，11) C. (45，7) D. (46，0)
-
科目： 来源： 题型：
查看答案和解析>>【题目】若10m=5，10n=3，则102m+3n= ．
【答案】675．
【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675，
故答案为：675.
点睛：此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则，可得102m+3n=102m×103n，然后根据幂的乘方的运算方法，可得102m×103n=（10m）2×（10n）3，最后把10m=5，10n=2代入化简后的算式，求出102m+3n的值是多少即可．
【题型】填空题
【结束】
18【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
)2 016×161 008； -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（ ）
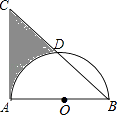
A.16
B.24﹣4π
C.32﹣4π
D.32﹣8π -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
)2 016×161 008；【答案】（1）﹣10m2n3+8m3n2；（2）2x﹣40；(3)1．
【解析】试题分析：（1）原式利用单项式乘以多项式法则计算即可得到结果；
（2）原式两项利用多项式乘以多项式法则计算，去括号合并即可得到结果；
（3）先根据幂的乘方的逆运算，把(－
)2 016化为(
)1008，再根据积的乘方的逆运算计算即可.试题解析：（1）原式=（5mn2）（﹣2mn）+（﹣4m2n）（﹣2mn）=﹣10m2n3+8m3n2；
（2）原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．
（3）原式=(
)1008×161 008=(
×16)1 008=1.【题型】解答题
【结束】
19【题目】如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．
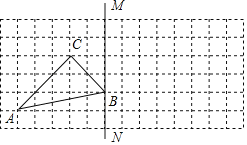
（1）画出△ABC关于直线BM对称的△A1B1C1；
（2）写出AA1的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，AB的垂直平分线DE交AC于D，垂足为E，若∠A=30°，CD=3．
（1）求∠BDC的度数．
（2）求AC的长度．
相关试题
