搜索
【题目】在矩形ABCD中 ，AB=8 , BC=6, 点P在边AB上。若将△DAP沿DP折叠 ，使点A落在矩形对角线上的点A，处，则AP的长为__________。
参考答案：
【答案】3或
【解析】①点A落在矩形对角线BD上，如图1所示。
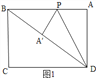
∵AB=8，AD=BC=6，∴BD=10，
根据折叠的性质,AD= 
=6,AP= 
,∠A= 
=90°，∴
=4，
设AP=x，则BP=8x，
∵
，∴(8x) =x+4，解得：x=3，∴AP=3；
②点A落在矩形对角线AC上，如图2所示：
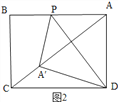
由折叠的性质可知PD垂直平分AA′，
∴∠BAC+∠
=∠PDA+∠
=90°.∴∠BAC=∠PDA.
∴tan∠BAC=tan∠PDA.∴
.
∴AP=
.综上所述AP的长为3或
.
故答案为：3或
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，直线y=﹣x+2与反比例函数y=
的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=
的图象有2个公共点，则b的取值范围是（ ）
A. b＞2 B. ﹣2＜b＜2 C. b＞2或b＜﹣2 D. b＜﹣2
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：
（1）如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ．
探索延伸：
（2）如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=
∠BAD，上述结论是否仍然成立，并说明理由．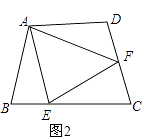 
-
科目： 来源： 题型：
查看答案和解析>>【题目】小丽想用一块面积为900 cm2的正方形纸片，沿着边的方向裁出一块面积为600 cm2的长方形纸片，使它的长宽之比为4∶3，她不知道是否裁得出来，正在发愁，小明见了说：“别发愁，一定能用这块正方形纸片裁出需要的长方形纸片．”你同意小明的说法吗？小丽能用这块纸片裁出符合要求的纸片吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若（x﹣2）2+|y+1|=0，则x+y等于（ ）
A.1
B.﹣1
C.3
D.﹣3 -
科目： 来源： 题型：
查看答案和解析>>【题目】某种商品每袋4.8元，在一个月内的销售量是m袋，用式子表示在这个月内销售这种商品的收入 ．
相关试题
