搜索
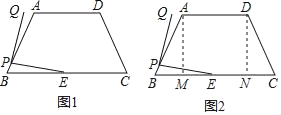
【题目】如图1，在四边形ABCD中，AD∥BC，AB=CD=13，AD=11，BC=21，E是BC的中点，P是AB上的任意一点，连接PE，将PE绕点P逆时针旋转90°得到PQ．
（1）如图2，过A点，D点作BC的垂线，垂足分别为M，N，求sinB的值；
（2）若P是AB的中点，求点E所经过的路径弧EQ的长（结果保留π）；
（3）若点Q落在AB或AD边所在直线上，请直接写出BP的长．
【答案】（1）
；（2）5π；（3）PB的值为
或
．
【解析】
（1）如图1中，作AM⊥CB用M，DN⊥BC于N，根据题意易证Rt△ABM≌Rt△DCN，再根据全等三角形的性质可得出对应边相等，根据勾股定理可求出AM的值，即可得出结论；
（2）连接AC，根据勾股定理求出AC的长，再根据弧长计算公式即可得出结论；
（3）当点Q落在直线AB上时，根据相似三角形的性质可得对应边成比例，即可求出PB的值；当点Q在DA的延长线上时，作PH⊥AD交DA的延长线于H，延长HP交BC于G，设PB=x，则AP=13﹣x，再根据全等三角形的性质可得对应边相等，即可求出PB的值.
解：（1）如图1中，作AM⊥CB用M，DN⊥BC于N．
∴∠DNM=∠AMN=90°，
∵AD∥BC，
∴∠DAM=∠AMN=∠DNM=90°，
∴四边形AMND是矩形，
∴AM=DN，
∵AB=CD=13，
∴Rt△ABM≌Rt△DCN，
∴BM=CN，
∵AD=11，BC=21，
∴BM=CN=5，
∴AM=
=12，
在Rt△ABM中，sinB=
=
．
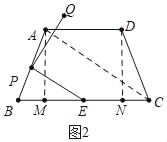
（2）如图2中，连接AC．
在Rt△ACM中，AC=
=
=20，
∵PB=PA，BE=EC，
∴PE=
AC=10，
∴
的长=
=5π．
（3）如图3中，当点Q落在直线AB上时，
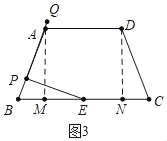
∵△EPB∽△AMB，
∴
=
=
，
∴
=
=
，
∴PB=
．
如图4中，当点Q在DA的延长线上时，作PH⊥AD交DA的延长线于H，延长HP交BC于G．
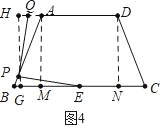
设PB=x，则AP=13﹣x．
∵AD∥BC，
∴∠B=∠HAP，
∴PG=
x，PH=（13﹣x），
∴BG=
x，
∵△PGE≌△QHP，
∴EG=PH，
∴
﹣
x=
（13﹣x），
∴BP=
．
综上所述，满足条件的PB的值为
或．
