【题目】如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE
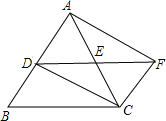
(1)图中的平行四边形有哪几个?请选择其中一个说明理由;
(2)若△AEF的面积是3,求四边形BCFD的面积.
参考答案:
【答案】(1)平行四边形ADCF,平行四边形BDFC,(2)12.
【解析】
试题分析:(1)由E为AC的中点,可得AE=CE,再由条件EF=DE 可得四边形ADCF是平行四边形;
(2)根据等底等高的三角形面积相等可得平行四边形对角线分成的四个小三角形面积相等可得△CEF的面积和△CED的面积都等于△AEF的面积为3,从而可得四边形BCFD的面积为12.
(1)图中的平行四边形有:平行四边形ADCF,平行四边形BDFC,
理由是:∵E为AC的中点,
∴AE=CE,
∵DE=EF,
∴四边形ADCF是平行四边形,
∴AD∥CF,AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,BD∥CF,
∴四边形BDFC是平行四边形.
(2)由(1)知四边形ADCF是平行四边形,四边形BDFC是平行四边形,
∴S△CEF=S△CED=S△AEF=3,
∴平行四边形BCFD的面积是12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m﹣2)x2+(m﹣1)x+m=0是一元二次方程的条件是( )
A.m≠l
B.m≠﹣1且m≠2
C.m≠2
D.m≠1且m≠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. a+2a=3a2B. (﹣a3)2=a6
C. a3a2=a6D. (a+b)2=a2+b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数a,b,定义a⊙b=3a+2b,则(x+y)⊙(x-y)化简后得_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD,CB相交于点H,E,AH=2CH.
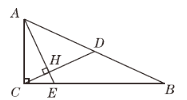
(1)求sin B的值;
(2)如果CD=
 ,求BE的值.
,求BE的值. -
科目: 来源: 题型:
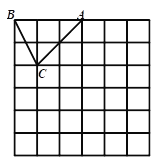
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 对角线相等的四边形是矩形B. 对角线互相垂直的四边形是正方形
C. 平行四边形的对角线平分一组对角D. 矩形的对角线相等且互相平分
相关试题

