搜索
【题目】二次函数y=ax2+bc+c的图象如图所示，则下列判断中错误的是（ ）
A. 图象的对称轴是直线x=﹣1 B. 当x＞﹣1时，y随x的增大而减小
C. 当﹣3＜x＜1时，y＜0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3，1
参考答案：
【答案】B
【解析】
直接根据二次函数的性质对各选项进行逐一分析即可．
A选项：∵抛物线与x轴的交点分别为-3，1，∴图象的对称轴是直线x=
=-1，故本选项正确；
B选项：∵抛物线开口向上，对称轴是直线x=-1，∴当x＜-1时，y随x的增大而减小，故本选项错误；
C选项：由函数图象可知，当-3＜x＜1时，y＜0，故本选项正确；
D选项：∵抛物线与x轴的交点分别为-3，1，∴一元二次方程ax2+bx+c=0的两个根是-3，1，故本选项正确．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图1，直线l1∥x轴，直线l2为第一、三象限的角平分线，直线l1与l2相交于A（3，3），点B为直越l1上一点，点C为x轴上一点，P（x，y）为一动点．
（1）当点P（x，y）在x轴上时，y= ，当点P（x，y）在直线l1上，y= ，当点P（x，y）在直线l2上时y= ．
如图1，当点P在直线l1下方、x轴上方、直线l2左上方区域时，x，y满足如下条件：
，则∠APO，∠PAB，∠POC的数量关系是 ．如图2，当点P在直线l1下方、x轴上方、直线l2右下方区域时，x，y满足如下条件：
，则∠APO，∠PAB，∠POC的数量关系是 ．（2）当点P在直线l1上方区域，且点P不在直线l2时，x，y满足的条件为：
，请画出图形，猜想∠APO，∠PAB，∠POC的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线 y=ax2+bx﹣
与 x 轴交于 A（1，0）、B（6，0）两点，D 是 y 轴上一点，连接 DA，延长 DA 交抛物线于点 E．（1）求此抛物线的解析式；
（2）若 E 点在第一象限，过点 E 作 EF⊥x 轴于点 F，△ADO 与△AEF 的面积比为
=
，求出点 E 的坐标；（3）若 D 是 y 轴上的动点，过 D 点作与 x 轴平行的直线交抛物线于 M、N 两点， 是否存在点 D，使 DA2=DMDN？若存在，请求出点 D 的坐标；若不存在，请说 明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一快递仓库里堆放着若干个相同的正方体快递件，管理员从正面看和从左面看这堆快递如图所示，则这正方体快递件最多有_____件.
-
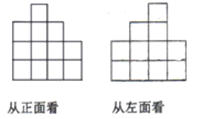
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明．
供选择的三个条件（请从其中选择一个）：
①AB=ED；
②BC=EF；
③∠ACB=∠DFE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）交于A，B两点，且点A的横坐标是-2，点B的横坐标是3，则以下结论：
①抛物线y=ax2（a≠0）的图象的顶点一定是原点；
②x＞0时，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）的函数值都随着x的增大而增大；
③AB的长度可以等于5；
④△OAB有可能成为等边三角形；
⑤当-3＜x＜2时，ax2+kx＜b，
其中正确的结论是（ ）
A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=________米.
相关试题
