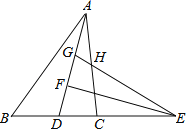
【题目】如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则![]() 的值为 .
的值为 .
参考答案:
【答案】![]() .
.
【解析】
试题分析:利用角平分线的性质,得到BD=![]() CD,延长AC,构造一对全等三角形△ABD≌△AMD;过点M作MN∥AD,构造平行四边形DMNG.由MD=BD=KD=
CD,延长AC,构造一对全等三角形△ABD≌△AMD;过点M作MN∥AD,构造平行四边形DMNG.由MD=BD=KD=![]() CD,得到等腰△DMK;然后利用角之间关系证明DM∥GN,从而推出四边形DMNG为平行四边形;由MN∥AD,列出比例式,求出
CD,得到等腰△DMK;然后利用角之间关系证明DM∥GN,从而推出四边形DMNG为平行四边形;由MN∥AD,列出比例式,求出![]() 的值.
的值.
解:已知AD为角平分线,则点D到AB、AC的距离相等,设为h.
∵![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴BD=![]() CD.
CD.
如右图,延长AC,在AC的延长线上截取AM=AB,则有AC=4CM.连接DM.
在△ABD与△AMD中,
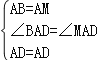
∴△ABD≌△AMD(SAS),
∴MD=BD=![]() CD.
CD.
过点M作MN∥AD,交EG于点N,交DE于点K.
∵MN∥AD,
∴![]() =
=![]() =
=![]() ,
,
∴CK=![]() CD,
CD,
∴KD=![]() CD.
CD.
∴MD=KD,即△DMK为等腰三角形,
∴∠DMK=∠DKM.
由题意,易知△EDG为等腰三角形,且∠1=∠2;
∵MN∥AD,
∴∠3=∠4=∠1=∠2,
又∵∠DKM=∠3(对顶角)
∴∠DMK=∠4,
∴DM∥GN,
∴四边形DMNG为平行四边形,
∴MN=DG=2FD.
∵点H为AC中点,AC=5CM,
∴![]() =
=![]() .
.
∵MN∥AD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在数轴l上,一动点Q从原点O出发,沿直线l以每秒钟2个单位长度的速度来回移动,其移动方式是先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…
(1)求出5秒钟后动点Q所处的位置;
(2)如果在数轴l上还有一个定点A,且A与原点O相距20个单位长度,问:动点Q从原点出发,可能与点A重合吗?若能,则第一次与点A重合需多长时间?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
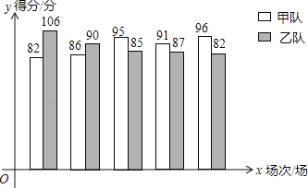
(1)、请根据统计图填写下表
平均数
中位数
方差
甲
乙
(2)、如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短?牧童最少要走多少m?
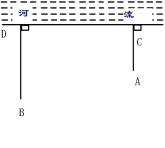
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,D为BC上一点,AD=DC=2,
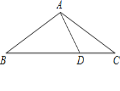
(1)求AC的长;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.

(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上到原点的距离等于2的点所表示的数是_______
相关试题

