【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
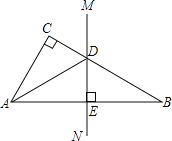
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
参考答案:
【答案】(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠CAD=20°,
∴∠ADC=70°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=35°,
答:∠B的度数是35°;
(2)∵∠C=90°,∠CAB=50°,
∴∠B=40°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=40°,
∴∠CAD=10°;
(3)设∠CAD=x,则∠DAB=∠B=2x,
则x+2x+2x=90°,
解得x=18,
则∠CAB=54°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:


请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=10,ab=5,则a2+b2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
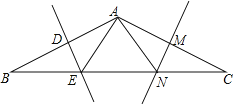
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.

(1)求证:AB=BE;
(2)连结OC,如果PD=
 ,∠ABC=
,∠ABC= ,求OC的长.
,求OC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一次函数y=3x﹣1的图象沿y轴向_____平移_____个单位后,得到的图象经过原点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣mx+6=0有一根是﹣3,那么这个方程的另一个根是( )
A.﹣5B.5C.﹣2D.2
相关试题

