【题目】如图,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
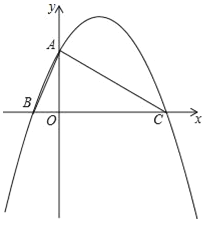
(1)求二次函数的解析式;
(2)判断△ABC的形状,并说明理由;
(3)若点H在x轴上运动,当以点A、H、C为顶点的三角形是等腰三角形时,请直接写出此时点H的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
参考答案:
【答案】(1)二次函数的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)△ABC是直角三角形;
(3)若点H在x轴上运动,当以点A、H、C为顶点的三角形是等腰三角形时,点H的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0);
,0);
(4)当t=3时,△AMN面积最大,此时点N的坐标为(3,0).
【解析】
试题分析:(1)将A、C两点的坐标代入y=ax2+![]() x+c,得到关于a、c的二元一次方程组,解方程组求出a、c的值,即可求得抛物线的解析式;
x+c,得到关于a、c的二元一次方程组,解方程组求出a、c的值,即可求得抛物线的解析式;
(2)先根据二次函数的解析式求出点B的坐标,再计算得出AB2+AC2=BC2,根据勾股定理的逆定理即可得出△ABC是直角三角形;
(3)设点H的坐标为(n,0),得出AC2=80,AH2=n2+16,HC2=(n﹣8)2=n2﹣16n+64.当以点A、H、C为顶点的三角形是等腰三角形时,分三种情况进行讨论:①AH=AC;②HC=AC;③AH=HC;分别列出关于n的方程,解方程即可;
(4)设点N的坐标为(t,0),那么BN=t+2,过M作MD⊥x轴于点D.根据平行线分线段成比例定理得出![]() ,求出MD=
,求出MD=![]() (t+2),再根据S△AMN=S△ABN﹣S△BMN,得出S△AMN=﹣
(t+2),再根据S△AMN=S△ABN﹣S△BMN,得出S△AMN=﹣![]() (t﹣3)2+5,根据二次函数的性质即可求解.
(t﹣3)2+5,根据二次函数的性质即可求解.
试题解析:(1)∵二次函数y=ax2+![]() x+c(a≠0)的图象过点A(0,4),C(8,0),
x+c(a≠0)的图象过点A(0,4),C(8,0),
∴![]() ,
,
解得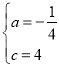 ,
,
∴二次函数的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)△ABC是直角三角形,理由如下:
∵y=﹣![]() x2+
x2+![]() x+4,
x+4,
∴当y=0时,﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0).
在Rt△AOB中,AB2=OA2+OB2=42+22=20,
在Rt△AOC中,AC2=OA2+OC2=42+82=80,
∵BC=OB+OC=2+8=10,
∴在△ABC中,AB2+AC2=20+80=100=102=BC2,
∴△ABC是直角三角形;
(3)设点H的坐标为(n,0),则AC2=80,AH2=n2+16,HC2=(n﹣8)2=n2﹣16n+64.
当以点A、H、C为顶点的三角形是等腰三角形时,可分三种情况:
①如果AH=AC,那么n2+16=80,解得n=±8(正值舍去),
此时点H的坐标为(﹣8,0);
②如果HC=AC,那么(n﹣8)2=80,解得n=8±4![]() ,
,
此时点H的坐标为(8+4![]() ,0)或(8﹣4
,0)或(8﹣4![]() ,0);
,0);
③如果AH=HC,那么n2+16=n2﹣16n+64,解得n=3,
此时点H的坐标为(3,0);
综上所述,若点H在x轴上运动,当以点A、H、C为顶点的三角形是等腰三角形时,点H的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0);
,0);
(4)设点N的坐标为(t,0),则BN=t+2,过M作MD⊥x轴于点D.
∵MD∥OA,
∴△BMD∽△BAO,
∴![]() ,
,
∵NM∥AC,
∴![]() ,
,
∴![]() ,
,
∵AO=4,BC=10,BN=t+2,
∴MD=![]() (t+2),
(t+2),
∴S△AMN=S△ABN﹣S△BMN
=![]() BNOA﹣
BNOA﹣![]() BNMD
BNMD
=![]() ×(t+2)×4﹣
×(t+2)×4﹣![]() ×(t+2)×
×(t+2)×![]() (t+2)
(t+2)
=﹣![]() t2+
t2+![]() t+
t+![]()
=﹣![]() (t﹣3)2+5,
(t﹣3)2+5,
∴当t=3时,△AMN面积最大,此时点N的坐标为(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,且B点的坐标为(4,2).

(1)画出△OAB向下平移3个单位后的△O1A1B1;
(2)画出△OAB绕点O逆时针旋转90°后的△OA2B2;
(3)求点B旋转到点B2所经过的路线长(结果保留根号和π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】去括号法则:若括号外的因数是正数,则去括号后________;若括号外的因数是负数,则去括号后________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集到的数据绘制成如下两幅不完整的图表(如表①,图②所示).
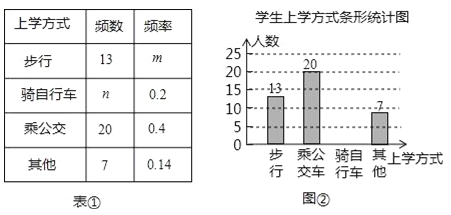
请根据图表中提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)补全条形统计图;
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx2+nx+p是y关于x的二次函数的条件是( )
A. m=0 B. m≠0 C. mnp≠0 D. m+n+p=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算器求sin 35°29'的值.(结果精确到0.001)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子可以用“=”连接的是( )
A. 5+4_______12-5 B. 7+(-4)______7-(+4)
C. 2+4(-2)______-12 D. 2(3-4)_____23-4
相关试题

