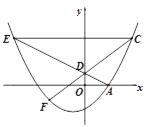
【题目】如图,抛物线![]() 与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E. 若点C(4,n)在抛物线上,且CE∥x轴.
与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E. 若点C(4,n)在抛物线上,且CE∥x轴.
(1)求m,n的值.
(2)连结CD并延长交抛物线于点F,求![]() 的值.
的值.
参考答案:
【答案】(1)m=1,n=4;(2)![]()
【解析】(1)∵点C(4,n)在抛物线上,∴x=4,代入抛物线得,n=4
令y=0,得![]() , 解得
, 解得![]() ∴A(2,0)
∴A(2,0)
∵CE∥x轴,∴将y=4代入![]() ,得
,得![]()
解得![]() ∴E(-6,4), 求得直线EC的解析式为
∴E(-6,4), 求得直线EC的解析式为![]()
当x=0时,y=1,∴m=1
(或作EG⊥x轴,得![]() ,∴m=1 )
,∴m=1 )
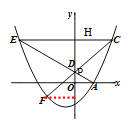
(2)作FP⊥y轴于P,
设直线CD的解析式为![]()
![]() 将C(4,4),D(0,1)代入上式得
将C(4,4),D(0,1)代入上式得![]() 解得
解得![]()
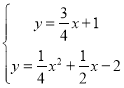 解得,
解得, ![]() ∴
∴![]()
∵CE∥FP,∴ ![]() ∴
∴ ![]()
-
科目: 来源: 题型:
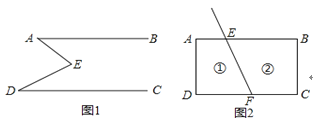
查看答案和解析>>【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算|﹣2|﹣30= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水资源保护组织对石家庄某小区的居民进行节约水资源的问卷调查.某居民在问卷上的选项代号画“√”,这个过程是收集数据中的( )
A.确定调查范围
B.汇总调查数据
C.实施调查
D.明确调查问题 -
科目: 来源: 题型:
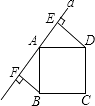
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为 .
相关试题

