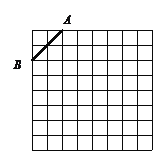
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标和△ABC的周长(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△DEC,连结AE和BD,试说明四边形ABDE是什么特殊四边形,并说明理由.
参考答案:
【答案】(1)图形见解析(2)![]()
![]() (3)矩形;
(3)矩形;
【解析】试题分析:(1)根据A点坐标为(-2,3),B点坐标为(-4,1),即可作出平面直角坐标系;
(2)由在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),根据勾股定理的逆定理即可求得点C坐标,然后求出周长即可;
(3)利用旋转的知识,画出画出相应的对应点即可.
试题解析:(1)坐标系如图;

(2)![]()
![]()
(3)画图正确;
矩形;
理由:由题目和旋转性质可知![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+mx+16=(x+4)2,则m的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“如果x2=y2”,那么“x=y”是______命題(填“真”成“假”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是一64的立方根,b的算术平方根为2.
(1)写出a,b的值;
(2)求3b一a的平方根,
-
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程:
(1)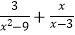 =1
=1
(2)2﹣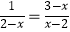 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】浙江卫视《中国好声音》总决赛,全国有7100人通过电视收看,这个数据用科学记数法表示为( )
A.71×102
B.7.1×102
C.7.1×103
D.0.71×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组数据不能作为直角三角形的三边长的是( )
A. 6、8、10 B. 5、12、13 C. 7、10、12 D. 3、4、5
相关试题

