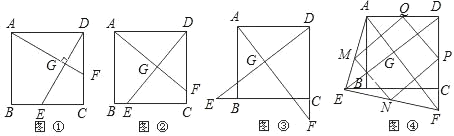
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
参考答案:
【答案】解:(1)成立;(2)成立.
![]() 四边形
四边形![]() 是正方形,
是正方形,![]() ,
,![]() .
.
又![]() ,
,![]() .
.![]() .
.
又![]() ,
,![]() .
.![]() ,
,![]() .
.
(3)正方形.证明:![]() ,
,
![]() ,同理
,同理![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
又![]() ,
,![]() .
.
又![]() ,
,![]() .
.![]() 平行四边形
平行四边形![]() 是菱形.
是菱形.
![]() .
.
又![]() ,
,![]() .
.![]() ,
,![]() 菱形
菱形![]() 是正方形.
是正方形.
【解析】
(1)根据正方形的性质证明△DEC≌△AFD即可知道结论成立.
(2)由已知得四边形ABCD为正方形,证明Rt△ADF≌Rt△ECD,然后推出∠ADE+∠DAF=90°;进而得出AF⊥DE;
(3)首先根据题意证明四边形MNPQ是菱形,然后又因为AF⊥DE,得出四边形MNPQ为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2020年元旦即将到来之际建湖县大润发和家乐福两超市准备提前庆祝该节日,分别推出如下促销方式:
大润发:全场均按八五折优惠;
家乐福:购物不超过200元,不给于优惠;超过了200元而不超过500元一律打八八折;超过500元时,其中的500元优惠12%,超过500元的部分打八折;
已知两家超市相同商品的标价都一样.
(1)当一次性购物总额是400元时,大润发、家乐福两家超市实付款分别是多少?
(2)当购物总额是多少时,大润发、家乐福两家超市实付款相同?
(3)某顾客在家乐福超市购物实际付款482元,试问该顾客的选择划算吗?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为
 .
.[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).

[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得
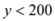 时,即
时,即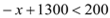 ,
, ∴解得
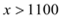
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)
 ,
,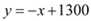 ,∴
,∴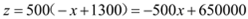
∵
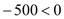 ,∴当
,∴当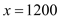 时,z最低,即
时,z最低,即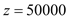 ;
;(3)利润
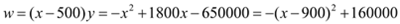
当
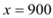 时,
时,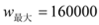 .
. 【题型】解答题
【结束】
23【题目】已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求
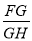 的值.
的值.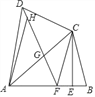
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(
 )写出扇形图中
)写出扇形图中 __________
__________ ,并补全条形图.
,并补全条形图.(
 )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.(
 )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有 人,如果体育中考引体向上达
人,如果体育中考引体向上达 个以上(含
个以上(含 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得7条折痕,那么对折四次可以得到 条折痕,如果对折
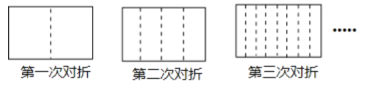 次,可以得到 条折痕.
次,可以得到 条折痕.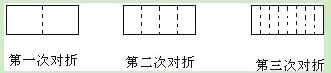
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

相关试题

