【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1). 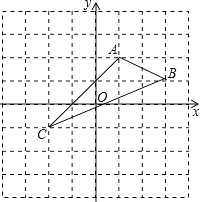
(1)在图中作出△ABC关于y轴对称的△A1B1C1 .
(2)写出A1 , B1 , C1的坐标(直接写出答案),
A1;B1;C1 .
(3)△A1B1C1的面积为 .
参考答案:
【答案】
(1)解:△A1B1C1如图所示
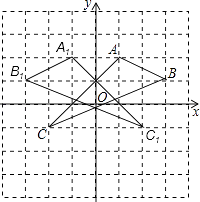
(2)(﹣1,2);(﹣3,1);(2,﹣1)
(3)4.5
【解析】解:(2)△A1(﹣1,2),B1(﹣3,1),C1(2,﹣1);(3)△A1B1C1的面积=5×3﹣ ![]() ×1×2﹣
×1×2﹣ ![]() ×2×5﹣
×2×5﹣ ![]() ×3×3,
×3×3,
=15﹣1﹣5﹣4.5,
=15﹣10.5,
=4.5.
故答案为:(2)(﹣1,2),(﹣3,1),(2,﹣1);(3)4.5.
(1)根据网格结构找出点A、B、C的对应点A1、B1、C1的位置,然后顺次连接即可;(2)根据平面直角坐标系写出各点的坐标;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有1个白球,2个黄球和3个红球,每个除颜色外完全相同,将球摇匀从中任取一球:(1)恰好取出白球;
(2)恰好取出红球;
(3)恰好取出黄球,
根据你的判断,将这些事件按发生的可能性从小到大的顺序排列 (只需填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( )

A.80°
B.100°
C.60°
D.45° -
科目: 来源: 题型:
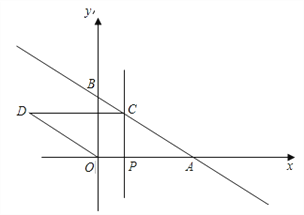
查看答案和解析>>【题目】如图,已知直线y=kx+b与x轴交于A(8,0),与y轴交于B(0,6),点P是x轴正半轴上的一动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造□OACD,设点P的横坐标为m.
(1)求直线AB的函数表达式;
(2)若四边形OACD恰是菱形,请求出m的值;
(3)在(2)的条件下,y轴的上是否存在点Q,连结CQ,使得∠OQC+∠ODC=180°.若存在,直接写出所有符合条件的点Q的坐标,若不存在,则说明理由.
-
科目: 来源: 题型:
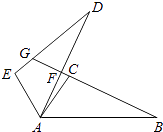
查看答案和解析>>【题目】如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC,
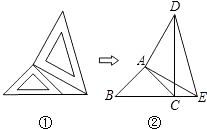
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE. -
科目: 来源: 题型:
查看答案和解析>>【题目】点M(﹣2,1)关于x轴对称的点的坐标是( )
A.(﹣2,﹣1)
B.(2.1)
C.(2,﹣1)
D.(1.﹣2)
相关试题

