Question

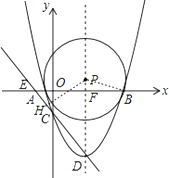
【题目】如图，已知二次函数y= x2﹣ x﹣3的图象与x轴交于A，B两点（点A在点B的左侧），与y轴的负半轴交于点C，顶点为D，作直线CD，点P是抛物线对称轴上的一点，若以P为圆心的圆经过A，B两点，并且和直线CD相切，则点P的坐标为

Answer 1

【答案】（4，0）或（4， ）
【解析】解：当y=0时， x2﹣ x﹣3=0，解得x1=﹣1，x2=9，则A（﹣1，0），B（9，0），
当x=0时，y= x2﹣ x﹣3=﹣3，则C（0，﹣3），
∵y= x2﹣ x﹣3= （x﹣4）2﹣ ，
∴抛物线的对称轴为直线x=4，D点坐标为（4，﹣ ），
设直线CD的解析式为y=kx+b，
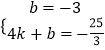把C（0，﹣3），D（4，﹣ ）代入得 ，解得 ，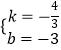
∴直线CD的解析式为y=﹣ x﹣3，
过P点作PH⊥直线CD于H，连结PB，CD交x轴于E点，抛物线的对称轴交x轴于F点，如图，则F（4，0），E（﹣ ，0），
∴EF=4﹣（﹣ ）= ，FB= ，
∴DE= = ，
设P（4，t），则PD=t+ ，PB= = ，
∵以P为圆心的圆经过A，B两点，并且和直线CD相切，
∴PH=PB= ，
∵∠PDH=∠EDF，
∴Rt△DPH∽Rt△DEF，
∴ = ，即 = ，
整理得8t2﹣75t=0，解得t1=0，t2= ，
∴P点坐标为（4，0）或（4， ）．
所以答案是（4，0）或（4， ）．

【考点精析】掌握二次函数的性质和切线的性质定理是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．