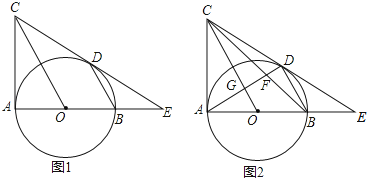
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)CD=6;(3)![]() .
.
【解析】
试题分析:(1)连接OD,如图1,利用平行线的性质得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,于是可根据“SAS”判定△CDO≌△CAO,则∠CDO=∠CAO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)设⊙O半径为r,则OD=OB=r,在Rt△ODE中利用勾股定理得到r2+42=(r+2)2,解得r=3,即OB=3,然后根据平行线分线段成比例定理,由DB∥OC得到DE:CD=BE:OB,于是可计算出CD=6;
(3)如图3,由△CDO≌△CAO得到AC=CD=6,在Rt△AOC中利用勾股定理计算出OC=3![]() ,再证明Rt△OAG∽△OCA,利用相似比计算出OG=
,再证明Rt△OAG∽△OCA,利用相似比计算出OG=![]() ,则CG=OC﹣OG=
,则CG=OC﹣OG=![]() ,易得BD=2OG=
,易得BD=2OG=![]() ,然后利用CG∥BD得到
,然后利用CG∥BD得到![]() =
=![]() =
=![]() .
.
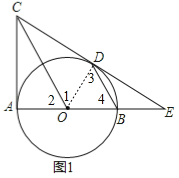
(1)证明:连接OD,如图1,
∵BD∥OC,
∴∠1=∠3,∠2=∠4,
又∵OD=OB,
∴∠3=∠4,
∴∠1=∠2,
在△CAO和△CDO中,
 ,
,
∴△CDO≌△CAO,
∴∠CDO=∠CAO=90°,
∴CD⊥OD,
∴CD是⊙O的切线;
(2)解:设⊙O半径为r,则OD=OB=r,
在Rt△ODE中,∵OD2+DE2=OE2,
∴r2+42=(r+2)2,解得r=3,
∴OB=3,
∵DB∥OC,
∴DE:CD=BE:OB,即4:CD=2:3,
∴CD=6;
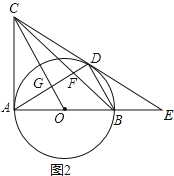
(3)解:如图3,
由(1)得△CDO≌△CAO,
∴AC=CD=6,
在Rt△AOC中,OC=![]() =
=![]() =3
=3![]() ,
,
∵∠AOG=∠COA,
∴Rt△OAG∽△OCA,
∴OA:OC=OG:OA,即3:3![]() =OG:3,
=OG:3,
∴OG=![]() ,
,
∴CG=OC﹣OG=3![]() ﹣
﹣![]() =
=![]() ,
,
∵OG∥BD,OA=OB,
∴OG为△ABD的中位线,
∴BD=2OG=![]() ,
,
∵CG∥BD,
∴![]() =
=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P1(-2,1)和P2(-2,-1),则P1和P2( )
A. 关于原点对称 B. 关于y轴对称 C. 关于x轴对称 D. 不存在对称关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以O为原点的平面直角坐标系中,已知点A(3,2)和点B(3,4),则△OAB的面积为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )

A.小于0.64m3 B.大于0.64m3 C.不小于0.64m3 D.不大于0.64m3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,-3)在第( )象限.
A. 一
B. 二
C. 三
D. 四
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
①abc>0;②a﹣b+c>0;③2a﹣3b=0;④c﹣4b>0.你认为其中正确信息是 (填序号).
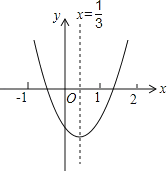
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣
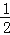 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.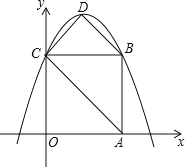
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
相关试题

