【题目】如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证: 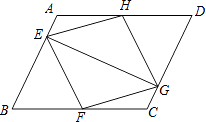
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
参考答案:
【答案】
(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
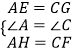 ,
,
∴△AEH≌△CGF(SAS)
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
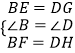
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形
【解析】(1)由全等三角形的判定定理SAS证得结论;(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为
 ,试求点P的坐标.
,试求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
 ×5=﹣
×5=﹣ =﹣249
=﹣249 ;
; 小军:原式=(49+
 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+ ×(﹣5)=﹣249
×(﹣5)=﹣249 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
 ×(﹣8)
×(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )

A. BC=FD,AC=ED B. ∠A=∠DEF,AC=ED
C. AC=ED,AB=EF D. ∠ABC=∠EFD,BC=FD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于
 MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
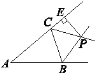
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图21所示,海岛上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸的距离相等吗?为什么?

相关试题

