Question

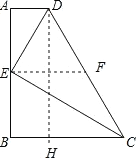
【题目】已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，．E是边AB的中点，联结DE、CE，且DE⊥CE．设AD=x，BC=y．

（1）如果∠BCD=60°，求CD的长；

（2）求y关于x的函数解析式，并写出自变量x的取值范围；

（3）联结BD．如果△BCD是以边CD为腰的等腰三角形，求x的值．

Answer 1

【答案】（1）4；　（2）x＞0，且；　（3）

【解析】（1）首先过点D作DH⊥BC，垂足为点H，由AD∥BC，AB⊥BC，DH⊥BC，可求得DH的长，然后设CH=x，则 CD=2x，利用勾股定理即可求得方程：x2+（2）2=4x2，解此方程即可求得答案；

（2）首先取CD的中点F，连接EF，由梯形的中位线，可表示出EF的长，易得四边形ABHD是平行四边形，然后由勾股定理可得：（y﹣x）2+12=（x+y）2，继而求得答案；

（3）分别从CD=BD或CD=BC去分析求解即可求得答案．

解：（1）过点D作DH⊥BC，垂足为点H．

∵AD∥BC，AB⊥BC，DH⊥BC，

∴DH=AB=2，

在Rt△DHC中，

∵∠BCD=60°，

∴∠CDH=30°．

∴CD=2CH，

设CH=x，则 CD=2x．

利用勾股定理，得 CH2+DH2=CD2．

即得：x2+（2）2=4x2．

解得 x=2（负值舍去）．

∴CD=4；

（2）取CD的中点F，连接EF，

∵E为边AB的中点，

∴EF=（AD+BC）=（x+y）．

∵DE⊥CE，

∴∠DEC=90°．

又∵DF=CF，

∴CD=2EF=x+y．

由AB⊥BC，DH⊥BC，得∠B=∠DHC=90°．

∴AB∥DH．

又∵AB=DH，

∴四边形ABHD是平行四边形．

∴BH=AD=x．

即得 CH=|y﹣x|，

在Rt△DHC中，利用勾股定理，得 CH2+DH2=CD2．

即得 （y﹣x）2+12=（x+y）2．

解得，

∴所求函数解析式为．

自变量x的取值范围是x＞0，且；

（3）当△BCD是以边CD为腰的等腰三角形时，有两种可能情况：CD=BD或CD=BC．

（ i）如果CD=BD，由DH⊥BC，得 BH=CH．即得 y=2x．

利用，得．

解得，．

经检验：，，且不合题意，舍去．

∴；

（ ii）如果CD=BC，则 x+y=y．

即得 x=0（不合题意，舍去），

综上可得：．

“点睛”此题属于四边形的综合题．考查了梯形的性质、平行四边形的判定与性质、等腰三角形的性质以及勾股定理等知识．注意掌握辅助线的作法，掌握方程思想与分类讨论思想的应用是解此题的关键．