【题目】已知抛物线y＝ax2﹣2ax+c(a＜0)的图象过点A(3，m)．

(1)当a＝﹣1，m＝0时，求抛物线的顶点坐标_____；

(2)如图，直线l：y＝kx+c(k＜0)交抛物线于B，C两点，点Q(x，y)是抛物线上点B，C之间的一个动点，作QD⊥x轴交直线l于点D，作QE⊥y轴于点E，连接DE．设∠QED＝β，当2≤x≤4时，β恰好满足30°≤β≤60°，a＝_____．

【答案】(1，4) ﹣

【解析】

（1）利用待定系数法求得抛物线解析式，然后利用配方法将抛物线解析式转化为顶点式，可以直接得到答案；

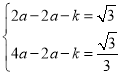（2）将点Q（x，y）代入抛物线解析式得到：y＝ax2﹣2ax+c．结合一次函数解析式推知：D（x，kx+c）．则由两点间的距离公式知QD＝ax2﹣2ax+c﹣（kx+c）＝ax2﹣（2a+k）x．在Rt△QED中，由锐角三角函数的定义推知tanβ＝＝ax﹣2a﹣k．所以tanβ随着x的增大而减小．结合已知条件列出方程组，解该方程组即可求得a的值．

(1)当a＝﹣1，m＝0时，y＝﹣x2+2x+c，A点的坐标为(3，0)，

∴﹣9+6+c＝0．

解得 c＝3．

∴抛物线的表达式为y＝﹣x2+2x+3．

即y＝﹣(x﹣1)2+4．

∴抛物线的顶点坐标为(1，4)，

故答案为(1，4)．

(2)∵点Q(x，y)在抛物线上，

∴y＝ax2﹣2ax+c．

又∵QD⊥x轴交直线 l：y＝kx+c(k＜0)于点D，

∴D点的坐标为(x，kx+c)．

又∵点Q是抛物线上点B，C之间的一个动点，

∴QD＝ax2﹣2ax+c﹣(kx+c)＝ax2﹣(2a+k)x．

∵QE＝x，

∴在Rt△QED中，tanβ＝＝ax﹣2a﹣k．

∴tanβ是关于x的一次函数，

∵a＜0，

∴tanβ随着x的增大而减小．

又∵当2≤x≤4时，β恰好满足30°≤β≤60°，且tanβ随着β的增大而增大，

∴当x＝2时，β＝60°；当x＝4时，β＝30°．

∴，

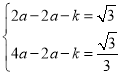解得，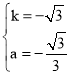

故答案为﹣．

关闭