【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
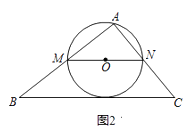
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
参考答案:
【答案】
(1)
解:∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴ ![]() ,即
,即 ![]() ;
;
∴AN= ![]() x;
x;
∴S=S△MNP=S△AMN= ![]()
![]() xx=
xx= ![]() x2.(0<x<4)
x2.(0<x<4)
(2)
解:如图2,设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD= ![]() MN.
MN.
在Rt△ABC中,BC= ![]() =5;
=5;
由(1)知△AMN∽△ABC,
∴ ![]() ,即
,即 ![]() ,
,
∴MN= ![]() x
x
∴OD= ![]() x,
x,
过M点作MQ⊥BC于Q,则MQ=OD= ![]() x,
x,
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴ ![]() ,
,
∴BM= ![]() x,AB=BM+MA=
x,AB=BM+MA= ![]() x+x=4
x+x=4
∴x= ![]() ,
,
∴当x= ![]() 时,⊙O与直线BC相切
时,⊙O与直线BC相切
(3)
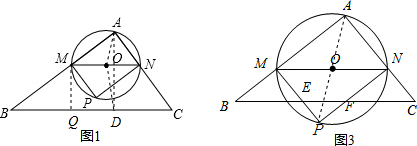
解:随点M的运动,当P点落在直线BC上时,连接AP,则O点为AP的中点.
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴ ![]() ,
,
∵AM=MB=2,
故以下分两种情况讨论:
①当0<x≤2时,y=S△PMN= ![]() x2,
x2,
∴当x=2时,y最大= ![]() ×4=
×4= ![]() ,
,
②当2<x<4时,设PM,PN分别交BC于E,F,
∵四边形AMPN是矩形,
∴PN∥AM,PN=M=x,
又∵MN∥BC,
∴四边形MBFN是平行四边形;
∴FN=BM=4﹣x,
∴PF=x﹣(4﹣x)=2x﹣4,
又∵△PEF∽△ACB,
∴ ![]() ,
,
∴S△PEF= ![]() (x﹣2)2;
(x﹣2)2;
y=S△MNP﹣S△PEF= ![]() x2﹣
x2﹣ ![]() (x﹣2)2=﹣
(x﹣2)2=﹣ ![]() x2+6x﹣6,
x2+6x﹣6,
当2<x<4时,y=﹣ ![]() x2+6x﹣6=﹣
x2+6x﹣6=﹣ ![]() (x﹣
(x﹣ ![]() )2+2,
)2+2,
∴当x= ![]() 时,满足2<x<4,y最大=2.
时,满足2<x<4,y最大=2.
综上所述,当x= ![]() 时,y值最大,最大值是2
时,y值最大,最大值是2
【解析】(1)由于三角形PMN和AMN的面积相当,那么可通过求三角形AMN的面积来得出三角形PMN的面积,求三角形AMN的面积可根据三角形AMN和ABC相似,根据相似比的平方等于面积比来得出三角形AMN的面积;(2)当圆O与BC相切时,O到BC的距离就是MN的一半,那么关键是求出MN的表达式,可根据三角形AMN和三角形ABC相似,得出MN的表达式,也就求出了O到BC的距离的表达式,如果过M作MQ⊥BC于Q,那么MQ就是O到BC的距离,然后在直角三角形BMQ中,用∠B的正弦函数以及BM的表达式表示出MQ,然后让这两表示MQ的含x的表达式相等,即可求出x的值;(3)要求重合部分的面积首先看P点在三角形ABC内部还是外面,因此可先得出这两种情况的分界线即当P落到BC上时,x的取值,那么P落点BC上时,MN就是三角形ABC的中位线,此时AM=2,因此可分两种情况进行讨论:
①当0<x≤2时,此时重合部分的面积就是三角形PMN的面积,三角形PMN的面积(1)中已经求出,即可的x,y的函数关系式.②当2<x<4时,如果设PM,PN交BC于E,F,那么重合部分就是四边形MEFN,可通过三角形PMN的面积﹣三角形PEF的面积来求重合部分的面积.不难得出PN=AM=x,而四边形BMNF又是个平行四边形,可得出FN=BM,也就有了FN的表达式,就可以求出PF的表达式,然后参照(1)的方法可求出三角形PEF的面积,即可求出四边形MEFN的面积,也就得出了y,x的函数关系式.然后根据两种情况得出的函数的性质,以及对应的自变量的取值范围求出y的最大值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
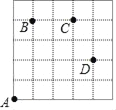
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
-
科目: 来源: 题型:
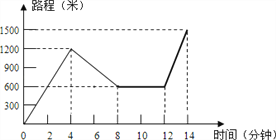
查看答案和解析>>【题目】小红星期天从家里出发汽车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到学校的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A.(9﹣7)x=1
B.(9+7)x=1
C.( +
+  )x=1
)x=1
D.( ﹣
﹣  )x=1
)x=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数
 ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
相关试题

