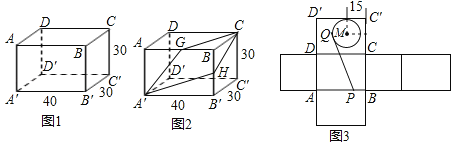
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
参考答案:
【答案】(1)①作图见试题解析;②往天花板ABCD爬行的最近路线A′GC更近;(2)![]() dm≤PQ≤55dm.
dm≤PQ≤55dm.
【解析】
试题分析:(1)①根据“两点之间,线段最短”可知:线段A′B为最近路线;
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①,运用勾股定理求出AC长;Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②,运用勾股定理求出A′C长,然后将两个长度进行比较,就可解决问题;
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.由⊙M与D′C′相切于点Q可得MQ⊥PQ,即∠MQP=90°,根据勾股定理可得PQ=![]() .要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
.要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
试题解析:(1)①根据“两点之间,线段最短”可知:线段A′B为最近路线,如图1所示.
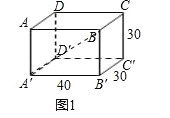
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①.
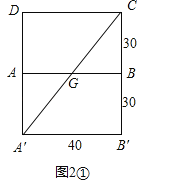
在Rt△A′B′C中,∠B′=90°,A′B′=40,B′C=60,∴AC=![]() =
=![]() =
=![]() ;
;
Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②.
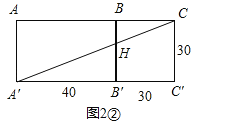
在Rt△A′C′C中,∠C′=90°,A′C′=70,C′C=30,∴A′C=![]() =
=![]() =
=![]() .∵
.∵![]() <
<![]() ,∴往天花板ABCD爬行的最近路线A′GC更近;
,∴往天花板ABCD爬行的最近路线A′GC更近;
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.
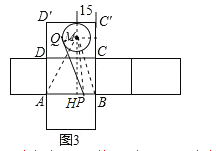
∵半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,BC′=60dm,∴MH=60﹣10=50,HB=15,AH=40﹣15=25,根据勾股定理可得AM=![]() =
=![]() =
=![]() ,MB=
,MB=![]() =
=![]() =
=![]() ,∴50≤MP≤
,∴50≤MP≤![]() .∵⊙M与D′C′相切于点Q,∴MQ⊥PQ,∠MQP=90°,∴PQ=
.∵⊙M与D′C′相切于点Q,∴MQ⊥PQ,∠MQP=90°,∴PQ=![]() .当MP=50时,PQ=
.当MP=50时,PQ=![]() =
=![]() ;
;
当MP=![]() 时,PQ=
时,PQ=![]() =55.
=55.
∴PQ长度的范围是![]() dm≤PQ≤55dm.
dm≤PQ≤55dm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设P=a2(﹣a+b﹣c),Q=﹣a(a2﹣ab+ac),则P与Q的关系是( )
A.P=Q
B.P>Q
C.P<Q
D.互为相反数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,AC,BD交于点O,若AB=6,AC=8,则BD的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
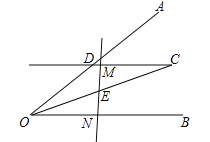
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句不是命题的是( )
A. 画两条相交直线 B. 互补的两个角之和是180°
C. 两点之间线段最短 D. 相等的两个角是对顶角
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成.求实际每天铺设管道的长度与实际施工天数.小宇同学根据题意列出方程
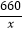 ﹣
﹣ 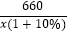 =6.则方程中未知数x所表示的量是( )
=6.则方程中未知数x所表示的量是( )
A.实际每天铺设管道的长度
B.实际施工的天数
C.原计划施工的天数
D.原计划每天铺设管道的长度
相关试题

