【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10 cm,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1cm的速度运动,同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动,在线段QC上取点E,使得QE =2cm,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,则①PE= cm,CE= (用含t的式子表示);
②求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。


参考答案:
【答案】(1)①5,2t -2;②BQ=![]() ;(2)存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12 s.
;(2)存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12 s.
【解析】试题分析:(1)①作AM⊥BC于M,由已知条件得出AB=AC,由等腰三角形的性质得出BM=CM,由直角三角形斜边上的中线性质得出AM=![]() BC=5,从而得出PE的长,由CQ=2t,QE=2,得到CE的长;
BC=5,从而得出PE的长,由CQ=2t,QE=2,得到CE的长;
②证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5﹣t,由CE=CQ﹣QE=2t﹣2得出方程,解方程即可;
(2)由平行四边形的判定得出AP=BE,得出方程,解方程即可.
试题解析:解:(1)①作AM⊥BC于M.∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,∴BM=CM,∴AM=![]() BC=5.∵PE⊥BC,∴PE=AM=5.∵AP=t,CQ=2t,∴CE=2t-2.
BC=5.∵PE⊥BC,∴PE=AM=5.∵AP=t,CQ=2t,∴CE=2t-2.
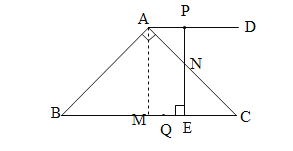
②由①可知:AM=![]() BC=5.∵AD∥BC,∴∠PAN=∠C=45°.∵PE⊥BC,∴PE=AM=5,PE⊥AD,∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5﹣t.∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,解得:t=
BC=5.∵AD∥BC,∴∠PAN=∠C=45°.∵PE⊥BC,∴PE=AM=5,PE⊥AD,∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5﹣t.∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,解得:t=![]() ,所以BQ=BC﹣CQ=10﹣2×
,所以BQ=BC﹣CQ=10﹣2×![]() =
=![]() ;
;
(2)存在,t=4;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,∴t=10﹣2t+2或t=2t﹣2﹣10
解得:t=4或12,∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径长为50cm,弦AB长50cm.求:点O到AB的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形(长方形),点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在线段BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 ____________________________________ .

-
科目: 来源: 题型:
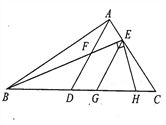
查看答案和解析>>【题目】如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E、F分别是AB、AC、BC的中点,
(1)若EF=10cm,则AB= cm;若BC=20cm,则DE= cm;
(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
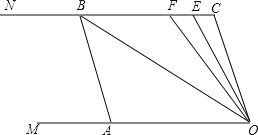
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
相关试题

