搜索
【题目】已知关于x的一元二次方程（k﹣2）2x2+（2k+1）x+1=0有两个不相等的实数根，则k的取值范围是（ ）
A.k＞ 
且k≠2
B.k≥ 且k≠2
C.k＞ 
且k≠2
D.k≥ 且k≠2
参考答案：
【答案】C
【解析】解：根据题意得k﹣2≠0且△=（2k+1）2﹣4（k﹣2）2＞0， 解得：k＞ 
且k≠2．
故选C．
【考点精析】本题主要考查了一元二次方程的定义和求根公式的相关知识点，需要掌握只有一个未知数，并且未知数的项的最高系数为2的方程为一元二次方程；根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】课堂上学习了勾股定理后，知道“勾三、股四、弦五”．王老师给出一组数让学生观察：3、4、5；5、12、13；7、24、25；9、40、41；…，学生发现这些勾股 数的勾都是奇数，且从 3 起就没有间断过，于是王老师提出以下问题让学生解决．
(1)请你根据上述的规律写出下一组勾股数：11、________、________；
(2)若第一个数用字母a(a为奇数，且a≥3)表示，那么后两个数用含a的代数式分别怎么表示？小明发现每组第二个数有这样的规律4=
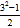，12=
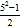，24=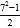
……，于是他很快表示了第二数为 
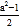，则用含a的代数式表示第三个数为________；(3)用所学知识证明你的结论．
-
科目： 来源： 题型：
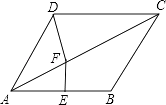
查看答案和解析>>【题目】如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，点E为垂足，连接DF，则∠CDF为（ ）
A.80°
B.70°
C.65°
D.60° -
科目： 来源： 题型：
查看答案和解析>>【题目】“低碳环保，绿色出行”的概念得到广大群众的接受，越来越多的人喜欢选择骑自行车作为出行工具．小军和爸爸同时骑车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆．小军始终以同一速度骑行，两人骑行的路程为y(米)与时间x(分钟)的关系如图．请结合图象，解答下列问题：
(1)填空：a=________；b=________；m=________．
(2)若小军的速度是 120 米/分，求小军第二次与爸爸相遇时距图书馆的距离．
(3)在(2)的条件下，爸爸自第二次出发后，骑行一段时间后与小军相距100 米，此时 小军骑行的时间为________分钟．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知四边形ABCD是菱形，△AEF是正三角形，E、F分别在BC、CD上，且EF=CD，则∠BAD= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为(0，2)，点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动，当点P与点B重合时停止运动，运动时间为t秒．
(1)当点P经过点C时，求直线DP的函数解析式；
(2)如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．
(3)点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：
（1）x2+2x﹣2=0
（2）3x2+4x﹣7=0
（3）（x+3）（x﹣1）=5
（4）（3﹣x）2+x2=9．
相关试题
