【题目】求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )
A.52017﹣1
B.52016﹣1
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:设S=1+5+52+53+…+52016 , 则5S=5+52+53+…+52017 ,
∴5S﹣S=52017﹣1,
∴S= ![]() .
.
故选C.
【考点精析】本题主要考查了数与式的规律的相关知识点,需要掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
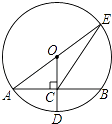
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2
B.8
C.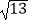
D.2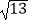
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )
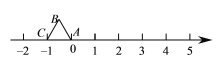
A. 不对应任何数 B. 对应的数是2010 C. 对应的数是2011 D. 对应的数是2012
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张等边三角形纸片沿各边中点剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;……,根据以上操作,若要得到100个小三角形,则需要操作的次数是( )

A. 25 B. 33 C. 34 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
相关试题

