【题目】对于满足0≤p≤4的一切实数,不等式x2+px>4x+p﹣3恒成立,则实数x的取值范围是_______.
参考答案:
【答案】x>3或x<﹣1
【解析】试题解析:令y=x2+px-(4x+p-3)=x2+px-3x-(x+p-3)
=x(x+p-3)-(x+p-3)
=(x-1)(x+p-3)>0
∴其解为 x>1 且 x>3-p①,或x<1 且x<3-p②,
因为 0≤p≤4,
∴-1≤3-p≤3,
在①中,要求x大于1和3-p中较大的数,而3-p最大值为3,故x>3;
在②中,要求x小于1和3-p中较小的数,而3-p最小值为-1,故x<-1;
故原不等式恒成立时,x的取值范围为:x>3或x<-1.
故答案为:x>3或x<-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理过程(补出缺项或在括号内注明理由,7分)
已知:△ABC,求证:∠A+∠B+∠C=180°
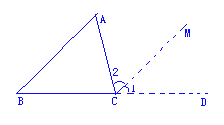
证明:延长BC到D,作CM∥AB
∴∠A=______ ( )
∠B=_______ ( )
∵∠2+∠1+∠ACB=180° ( )
∴___________________( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
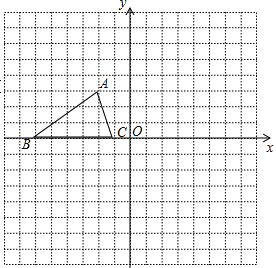
(1)请直接写出点A关于y轴对称的点的坐标:______
(2)将△ABC绕坐标原点O逆时针旋转90°.画出图形,直接写出点B的对应点的坐标:___________
(3)请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标:____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1)本次调查共抽取了 天的空气质量检测结果,请补全条形统计图;
(2)扇形统计图中3级空气质量所对应的圆心角为 °;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,请你估计2015年该城市有多少天不适宜开展户外活动.(说明:2015年共365天)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣3(x﹣2y)+4(x﹣2y)的结果是( )
A. x﹣2y B. x+2y C. ﹣x﹣2y D. ﹣x+2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式(x﹣4)2=x2﹣8x+m2成立,则m的值是()
A. 16B. 4C. ﹣4D. 4或﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】数-3的相反数是______________
相关试题

