【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ![]() ,则⊙O的半径为( )
,则⊙O的半径为( ) 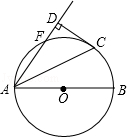
A.2 ![]()
B.4 ![]()
C.2
D.4
参考答案:
【答案】D
【解析】解:连结BC,如图, ∵AB为直径,
∴∠ACB=90°,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴∠BOC= ![]() ×180°=60°,
×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=2 ![]() ,
,
∴AC=2CD=4 ![]() ,
,
在Rt△ACB中,BC2+AC2=AB2 ,
即(4 ![]() )2+(
)2+( ![]() AB)2=AB2 ,
AB)2=AB2 ,
∴AB=8,
∴⊙O的半径为4.
故选D.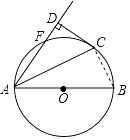
【考点精析】解答此题的关键在于理解圆心角、弧、弦的关系的相关知识,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )
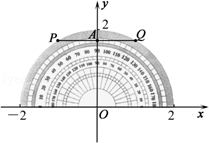
A.(﹣1, )
)
B.(0, )
)
C.( ,0)
,0)
D.(1, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
-
科目: 来源: 题型:
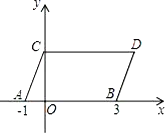
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,.B 的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2) 在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
相关试题

