【题目】AB∥CD,点C在点D的右侧,∠ABC 、∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.
(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.

参考答案:
【答案】(1)∠BED=![]() n°+40°;(2)∠BED的度数改变,∠BED=220°﹣
n°+40°;(2)∠BED的度数改变,∠BED=220°﹣![]() n°.
n°.
【解析】试题分析:(1)如图1,过点E作EF∥AB,根据平行线性质可得∠ABE=∠BEF,∠CDE=∠DEF,再由角平分线定义得出∠ABE=![]() ∠ABC
∠ABC![]() =n°,∠CDE=
=n°,∠CDE=![]() ∠ADC=40°,代入∠BED=∠BEF+∠DEF即可求得答案;
∠ADC=40°,代入∠BED=∠BEF+∠DEF即可求得答案;
(2)如图2,过点E作EF∥AB,根据角平分线定义可得∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,再由平行线性质可得∠BEF=180°﹣∠ABE=180°﹣
∠ADC=40°,再由平行线性质可得∠BEF=180°﹣∠ABE=180°﹣![]() n°,∠CDE=∠DEF=40°,代入∠BED=∠BEF+∠DEF即可求得答案.
n°,∠CDE=∠DEF=40°,代入∠BED=∠BEF+∠DEF即可求得答案.
试题解析:解:(1)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,
∠ADC=40°,
∴∠BED=∠BEF+∠DEF=![]() n°+40°;
n°+40°;
(2)∠BED的度数改变,
过点E作EF∥AB,如图,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,
∠ADC=40°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣![]() n°,∠CDE=∠DEF=40°,
n°,∠CDE=∠DEF=40°,
∴∠BED=∠BEF+∠DEF=180°﹣![]() n°+40°=220°﹣
n°+40°=220°﹣![]() n°.
n°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年春运期间,全国有23.2亿人次进行东西南北大流动,用科学记数法表示23.2亿是( )
A.23.2×108 B.2.32×109 C.232×107 D.2.32×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要了解八年级学生的视力情况,在全校八年级240名学生中随机抽取了25名学生进行检测,在这个问题中,样本容量是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程5x﹣y=7,用含x的代数式表示y,y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE.
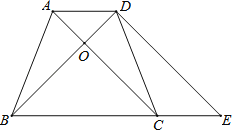
(1)求证:BD=DE.
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
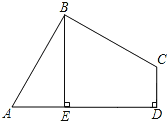
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
相关试题

