【题目】我校数学兴趣小组的同学要测量建筑物的高度，如图，建筑物前有一段坡度为的斜坡，小明同学站在斜坡上的点处，用测角仪测得建筑物屋顶的仰角为，接着小明又向下走了米，刚好到达坡底处，这时测到建筑物屋顶的仰角为，、、、、、在同一平面内．若测角仪的高度米，则建筑物的高度约为（ ）．（精确到0.1米，参考数据：，，）

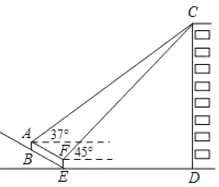
A.38.6B.39.0C.40.0D.41.5

【答案】D

【解析】

设CD＝x米．延长AB交DE于H，作AM⊥CD于M，FN⊥CD于N，求出BH＝4（米），EH＝8（米），由矩形的性质得出AM＝DH，AH＝DM，FN＝DE，FE＝DN＝1.5（米），在Rt△CFN中，求出CN＝FN＝DE＝（x－1.5）（米），AM＝DH＝（8＋x－1.5）（米），CM＝（x－5.5）（米），在Rt△ACM中，由AM＝，得出方程，解方程即可．

解：如图，延长AB交DE于H，作AM⊥CD于M，FN⊥CD于N，设CD＝x米．

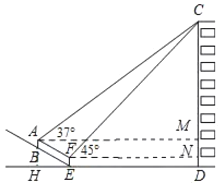
∵在Rt△BHE中，BE＝4米，BH：EH＝1：2，

∴BH＝4（米），EH＝8（米），

∵四边形AHDM是矩形，四边形FEDN是矩形，

∴AM＝DH，AH＝DM，FN＝DE，FE＝DN＝1.5（米），

∵在Rt△CFN中，∠CFN＝45°，

∴CN＝FN＝DE＝（x－1.5）（米），

∵AM＝DH＝（8＋x－1.5）（米），CM＝（x－5.5）（米），

∵在Rt△ACM中，∠CAM＝37°，

∴AM＝，

∴8＋x－1.5≈，

∴x≈41.5（米），

∴CD≈41.5米，

故选：D．

关闭