【题目】已知关于![]() 的方程
的方程![]() 的两个实数根的平方和是
的两个实数根的平方和是![]() ,则
,则![]() ________.
________.
参考答案:
【答案】![]()
【解析】
设方程![]() 的两个实数根分别为m、n,根据根与系数的关系可得出m+n=-2k-1,mn=k2,结合m2+n2=7即可得出关于k的一元二次方程,解方程可得出k的值,再根据方程两个实数根,结合根的判别式即可得出关于k的一元一次不等式,解不等式可得出k的取值范围,由此即可确定k的值.
的两个实数根分别为m、n,根据根与系数的关系可得出m+n=-2k-1,mn=k2,结合m2+n2=7即可得出关于k的一元二次方程,解方程可得出k的值,再根据方程两个实数根,结合根的判别式即可得出关于k的一元一次不等式,解不等式可得出k的取值范围,由此即可确定k的值.
设方程![]() 的两个实数根分别为m、n,则有:m+n=-2k-1,mn=k2,
的两个实数根分别为m、n,则有:m+n=-2k-1,mn=k2,
∵m2+n2=(m+n)2-2mn=7,
∴(-2k-1)2-2k2=7,即k2+2k-3=0,
解得:k=-3或k=1.
∵方程有实数根,
∴△=(2k+1)2-4k2=4k+1≥0,
∴k≥-![]() ,
,
∴k=1.
故答案为:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低
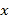 元.
元.(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两块完全相同的含30°的直角三角板叠放在一起,且∠DAB=30°,有以下四个结论,①AF⊥BC;②∠BOE=135°;③O为BC中点;④AG:DE=1:3,其中正确结论的序号是( )
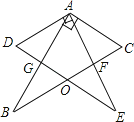
A.①②B.②④C.②③D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 、
、 ,点
,点 坐标为
坐标为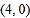 .
. 求该抛物线的解析式;
求该抛物线的解析式; 抛物线的顶点为
抛物线的顶点为 ,在
,在 轴上找一点
轴上找一点 ,使
,使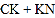 最小,并求出点
最小,并求出点 的坐标;
的坐标; 点
点 是线段
是线段 上的动点,过点
上的动点,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 .当
.当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标; 若平行于
若平行于 轴的动直线
轴的动直线 与该抛物线交于点
与该抛物线交于点 ,与直线
,与直线 交于点
交于点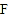 ,点
,点 的坐标为
的坐标为 .问:是否存在这样的直线
.问:是否存在这样的直线 ,使得
,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程 .
. 若
若 是方程的一个根,求
是方程的一个根,求 的值和方程的另一根;
的值和方程的另一根; 当
当 为何实数时,方程有实数根;
为何实数时,方程有实数根; 若
若 ,
, 是方程的两个根,且
是方程的两个根,且 ,试求实数
,试求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简:[x(x2y2﹣xy)﹣2y(x2﹣x3y)]÷3x2y
(2)化简求值:(x+2y)2﹣(x﹣2y)2﹣(x+2y)(x﹣2y)﹣4y2,其中y=1,x=
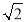 .
.
相关试题

