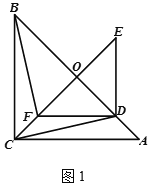
【题目】阅读材料：如图，与都是等腰直角三角形，且点在边上，，的中点均为，连接，，，显然，点，，在同一条直线上，可以证明，所以

解决问题：

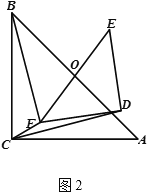
（1） 将图中的绕点旋转到图的位置， 猜想此时线段与的数量关系，并证明你的结论．

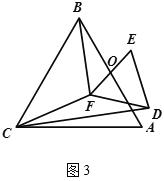
（2） 如图，若与都是等边三角形，，的中点均为，上述中结论仍然成立吗？如果成立，请说明理由；如果不成立，请求出与之间的数量关系．

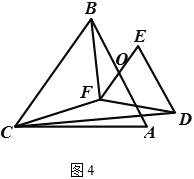
（3） 如图， 若与都是等腰三角形，，的中点均为，且顶角，与之间的数量关系如何（用含的式子表示出来）？请直接写出结果．

【答案】（1），证明见解析；（2）（1）中的结论不成立，为；（3）

【解析】

（1）如答图②所示，连接OC、OD，由全等三角形的判定定理SAS证明△BOF≌△COD；

（2）如答图③所示，连接OC、OD，由等边三角形的性质和锐角三角函数的定义推知，结合∠BOF＝∠COD即可证明△BOF∽△COD，相似比为；
（3）如答图④所示，连接OC、OD，由等边三角形的性质和锐角三角函数的定义推知，结合∠BOF＝∠COD即可证明△BOF∽△COD，相似比为tan．

解：（1）猜想：，

证明如下：连接，，如解图所示


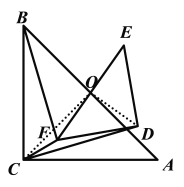
解图1

为等腰直角三角形，点为斜边的中点，

，

为等腰直角三角形，点为斜边的中点，

，，

，

，

，

在与中，，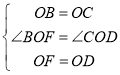

，

；

（2）中的结论不成立

连接，，如解图所示

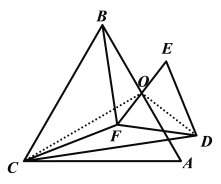
解图2

为等腰直角三角形，点为斜边的中点，

，，

为等腰直角三角形，点为斜边的中点，

，，

，

，

，

，

在与中，，

；

（3）如解图3所示，连接OC、OD，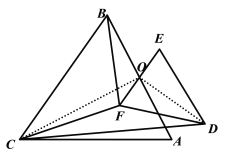

解图3
∵△ABC为等腰三角形，点O为底边AB的中点，
∴，∠BOC＝90°，
∵△DEF为等腰三角形，点O为底边EF的中点，
∴，∠DOF＝90°，
∴，
∵∠BOF＝∠BOC＋∠COF＝90°＋∠COF，∠COD＝∠DOF＋∠COF＝90°＋∠COF，
∴∠BOF＝∠COD，
在△BOF与△COD中，
∵，∠BOF＝∠COD，
∴△BOF∽△COD，
∴．

关闭