【题目】△ABC的两条中线AD、BE交于点F,连接CF,若△ABC的面积为24,则△ABF的面积为( )

A. 10 B. 8 C. 6 D. 4
参考答案:
【答案】B
【解析】由中线得:S△ABD=S△ADC得S△ABD=S△ABE,由已知S△ABC=24,得出△ABE和△ABD的面积为12,根据等式性质可知S△AEF=S△BDF,结合中点得:S△AEF=S△EFC=S△DFC=![]() S△ADC,相当于把△ADC的面积平均分成三份,每份为4,由此可得S△ABF=S△ABD-S△BDF.
S△ADC,相当于把△ADC的面积平均分成三份,每份为4,由此可得S△ABF=S△ABD-S△BDF.
∵AD是中线,
∴S△ABD=S△ADC=![]() S△ABC,
S△ABC,
∵S△ABC=24,
∴S△ABD=S△ADC=![]() ×24=12,
×24=12,
同理S△ABE=12,
∴S△ABD=S△ABE,
∴S△ABD-S△ABF=S△ABE-S△ABF,
即S△AEF=S△BDF,
∵D是中点,
∴S△BDF=S△DFC,
同理S△AEF=S△EFC,
∴S△AEF=S△EFC=S△DFC=![]() S△ADC=
S△ADC=![]() ×12=4,
×12=4,
∴S△ABF=S△ABD-S△BDF=12-4=8,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )

A. =
= 
B. =
= 
C. =
= 
D. =
= 
-
科目: 来源: 题型:
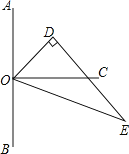
查看答案和解析>>【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC与△A′B′C′中,有下列条件:(1)
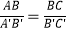 ,(2)
,(2) 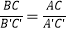 ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点(小正方形的顶点叫格点)上,连接BD.

(1)利用格点在图中画出△ABD中AD边上的高,垂足为H.
(2)①画出将△ABD先向右平移2格,再向上平移2格得到的△A1B1D1;
②平移后,求线段AB扫过的部分所组成的封闭图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论:①AE+BF=AC,②AE2+BF2=EF2,③S四边形CEDF=
 S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
A. ①②③④ B. ①②③ C. ①④ D. ②③
相关试题

