【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D、E分别在AC、BC边上,且∠DOE=90°,DE交OC于P,下列结论:
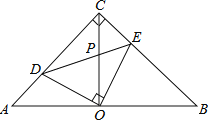
①图中的全等三角形共有3对;
②AD=CE;
③∠CDO=∠BEO;
④OC=DC+CE;
⑤△ABC的面积是四边形DOEC面积的2倍.
正确的是 .(填序号)
参考答案:
【答案】①②③⑤
【解析】
试题分析:根据等腰三角形的性质,直角三角形斜边上的中线性质,三角形内角和定理,等腰三角形的性质得出∠A=∠B=45°,CO=AO=BO,CO⊥AB,∠ACO=∠BCO=45°,求出∠A=∠ECO,∠B=∠DCO,∠COA=∠COB=90°,∠AOD=∠COE,∠COD=∠BOE,根据ASA推出△COE≌△AOD,△COD≌△BOE,根据全等三角形的性质得出S△COE=S△AOD,AD=CE,∠CDO=∠BEO,再逐个判断即可.
解:∵在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,
∴∠A=∠B=45°,CO=AO=BO,CO⊥AB,∠ACO=∠BCO=45°,
∴∠A=∠ECO,∠B=∠DCO,∠COA=∠COB=90°,
∵∠DOE=90°,
∴∠AOD=∠COE=90°﹣∠COD,∠COD=∠BOE=90°﹣∠COE,
在△COE和△AOD中
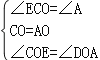
∴△COE≌△AOD(ASA),
同理△COD≌△BOE,
∴S△COE=S△AOD,AD=CE,∠CDO=∠BEO,△ABC的面积是四边形DOEC面积的2倍,
在△AOC和△BOC中
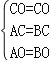
∴△AOC≌△BOC,
∵AD=CE,
∴CD+CE=AC,
∵∠COA=90°,
∴CO<AC,
∴OC=DC+CE错误;
即①②③⑤正确,④错误;
故答案为:①②③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM平分∠AOB,MC∥OB,MD⊥OB于D,若∠OMD=75°,OC=8,则MD的长为( )

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
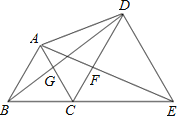
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为 .
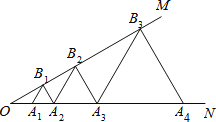
-
科目: 来源: 题型:
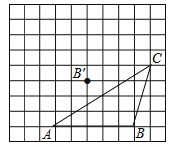
查看答案和解析>>【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 正数和负数统称有理数 B. 正整数和负整数统称为整数
C. ﹣a是负数 D. 整数和分数统称为有理数
-
科目: 来源: 题型:
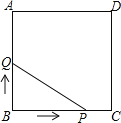
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
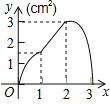 B.
B.
C.
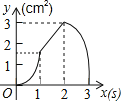 D.
D.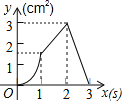
相关试题

