【题目】已知,如图,在平行四边形ABCD中,BF平分![]() 交AD于点F,AE
交AD于点F,AE![]() BF于点O,交BC于点E,连接EF.
BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=3,求四边形ABCD的面积.

参考答案:
【答案】(1)答案见解析;(2) ![]() .
.
【解析】
(1)由BF平分∠ABC得到∠ABF=∠EBF,由AD∥BC,得到∠EBF=∠AFB,进而得到△ABF为等腰三角形,得到AB=AF;由AE⊥BF,可证明△ABO≌△EBO,得到BE=AB,进而可证明四边形ABEF为菱形;
(2)由(1)中四边形ABEF为菱形,过A点作AH⊥BC于H点,根据菱形等面积法求出AH的长,进而求出平行四边形ABCD的高,进而求出其面积.
解:(1)证明:∵四边形ABCD为平行四边形,且F在AD上,E在BC上
∴AF∥BE
∴∠EBF=∠AFB
∵BF是∠ABE的角平分线
∴∠EBF=∠ABF
∴∠ABF=∠AFB
∴△ABF为等腰三角形,且AF=AB
又AE⊥BF,∴∠AOB=∠EOB=90°
在△AOB和△EOB中:
 ,∴△AOB和△EOB(ASA)
,∴△AOB和△EOB(ASA)
∴AB=BE
又AB=AF
∴BE=AF,且BE∥AF,∴四边形ABEF为平行四边形
又AB=BE,∴四边形ABEF为菱形.
(2)过A点作AH⊥BC于H点,如下图所示

∵四边形ABEF为菱形
∴AE⊥BF,且BO=![]() BF=4,OE=
BF=4,OE=![]() AE=3
AE=3
∴在Rt△BOE中:![]()
由菱形等面积法:![]() ,代入数据得:
,代入数据得:
AH=![]()
∴平行四边形ABCD的高为![]()
∴![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
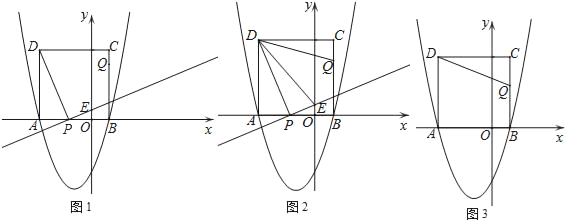
查看答案和解析>>【题目】如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B(1,0),以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.
(1)求二次函数的解析式及点A的坐标;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,并求出这个最大值;
(3)在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;
(4)是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?若存在,请求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
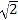 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此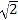 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<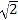 <2,所以
<2,所以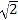 的整数部分为1,将
的整数部分为1,将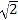 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分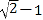 ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:(1)
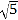 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;(2)
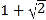 的整数部分是______,小数部分是_____;
的整数部分是______,小数部分是_____;(3)若设
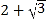 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣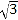 y的值.
y的值. -
科目: 来源: 题型:
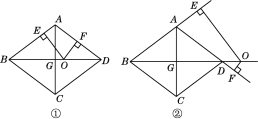
查看答案和解析>>【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.

相关试题

