【题目】已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位,求平移后的图象的解析式;
(3) 在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图像回答:当直线y=0.5x+b (b<k)与此图象有两个公共点时,b的取值范围.
参考答案:
【答案】(1)k=1,2,3;
(2)图象的解析式为y=2x2+4x-6;
(3)b(b<3)的取值范围为-0.5<b<1.5.
【解析】解:(1)由题意得,Δ=16-8(k-1)≥0.∴k≤3.∵k为正整数,∴k=1,2,3.
(2)当k=1时,方程2x2+4x+k-1=0有一个根为零;
当k=2时,方程2x2+4x+k-1=0无整数根;
当k=3时,方程2x2+4x+k-1=0有两个非零的整数根.
综上所述,k=1和k=2不合题意,舍去;k=3符合题意.
当k=3时,二次函数为y=2x2+4x+2,把它的图象向下平移8个单位长度得到的图象的解析式为y=2x2+4x-6.
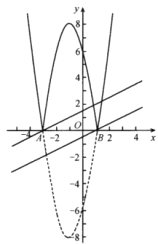
(3)设二次函数y=2x2+4x-6的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
当直线y=0.5x+b经过A点时,可得b=1.5;
当直线y=0.5x+b经过B点时,可得-0.5.
由图象可知,符合题意的b(b<3)的取值范围为-0.5<b<1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm)
160
165
170
175
180
学生人数(人)
1
3
2
2
2
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm -
科目: 来源: 题型:
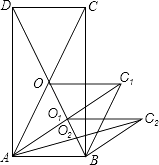
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
A. cm2
cm2
B. cm2
cm2
C.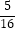 cm2
cm2
D. cm2
cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则它是_________ 边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某航空母舰的满载排水量为60900吨.将数60900用科学记数法表示为( )
A. 0.609×105 B. 6.09×104 C. 60.9×103 D. 609×102
-
科目: 来源: 题型:
查看答案和解析>>【题目】有n个数,第一个记为a1,第二个.记为a2;……,第n个记为ax,若 a1=
 ,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”(1)则a2=______;a3 =______;a4 =______.
(2)根据(1)的计算结果,猜想a2005=______;a2006=______.
(3)计算:
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数a,b之间的一种运算,记作(a,b):如果

 ,那么(a,b)=c.
,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,
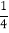
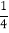 )=_______.
)=_______.(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
相关试题

