【题目】如图,已知抛物线y=﹣![]() x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
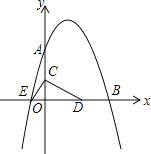
(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
参考答案:
【答案】(1)y=﹣![]() x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=
x2+3x+8,E(﹣2,0);(2)当t=5时,S最大=![]() .
.
【解析】
试题分析:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c即可求出抛物线的解析式为:y=﹣
x2+bx+c即可求出抛物线的解析式为:y=﹣![]() x2+3x+8;再令y=0,得:﹣
x2+3x+8;再令y=0,得:﹣![]() x2+3x+8=0,解方程可得点E的坐标;
x2+3x+8=0,解方程可得点E的坐标;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8﹣t,然后令y=0,点E的坐标为(﹣2,0),进而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:S=﹣![]() t2+5t,然后转化为顶点式即可求出最值为:S最大=
t2+5t,然后转化为顶点式即可求出最值为:S最大=![]() .
.
解:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c得:
x2+bx+c得: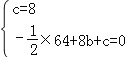 ,
,
解得:b=3,c=8,
故抛物线的解析式为:y=﹣![]() x2+3x+8,
x2+3x+8,
∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣![]() x2+3x+8=0,
x2+3x+8=0,
解得:x1=8,x2=﹣2,
∵点E在x轴的负半轴上,
∴点E(﹣2,0),
∴OE=2;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=﹣
(10﹣t)t=﹣![]() t2+5t,
t2+5t,
即S=﹣![]() t2+5t=﹣
t2+5t=﹣![]() (t﹣5)2+
(t﹣5)2+![]() ,
,
∴当t=5时,S最大=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是( ).
A.18 B.15 C.18或15 D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木棒的长度分别是5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况有( )
A.3种 B.4种 C.5种 D.6种
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三根小木棒能构成三角形的是( )
A. 2cm,3cm,5cm B. 7cm,4cm,2cm
C. 3cm,4cm,8cm D. 3cm,4cm,4cm
-
科目: 来源: 题型:
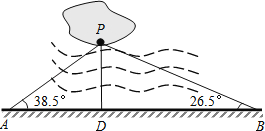
查看答案和解析>>【题目】如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
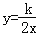 和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.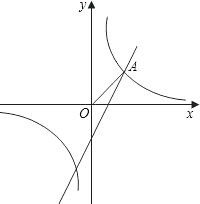
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
相关试题

